题目内容
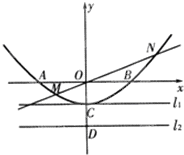 如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线
如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线l1、l2.
(1)求抛物线对应的二次函数的解析式;
(2)求证以ON为直径的圆与直线l1相切;
(3)求线段MN的长(用k表示),并证明M、N两点到直线l2的距离之和等于线段MN的长.
分析:(1)设函数解析式为y=ax2+bx+c,然后利用待定系数法求解即可;
(2)设M(x1,y1),N(x2,y2),然后代入抛物线方程,用含y2的式子表示出ON,设ON的中点E,分别过点N、E向直线l、作垂线,垂足为P、F,利用梯形的中位线定理可得出EF,与所求ON的值进行比较即可得出结论;
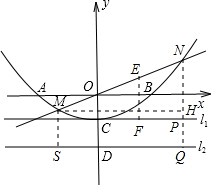
(3)过点M作MH丄NP交NP于点H,在RT△MNH中表示出MN2,结合直线方程将MN2化简,求出MN,然后延长NP交l2于点Q,过点M作MS丄l2交l2于点S,则可证M、N两点到直线l2的距离之和等于线段MN的长.
(2)设M(x1,y1),N(x2,y2),然后代入抛物线方程,用含y2的式子表示出ON,设ON的中点E,分别过点N、E向直线l、作垂线,垂足为P、F,利用梯形的中位线定理可得出EF,与所求ON的值进行比较即可得出结论;
(3)过点M作MH丄NP交NP于点H,在RT△MNH中表示出MN2,结合直线方程将MN2化简,求出MN,然后延长NP交l2于点Q,过点M作MS丄l2交l2于点S,则可证M、N两点到直线l2的距离之和等于线段MN的长.
解答:(1)解:设抛物线对应二次函数的解析式为y=ax2+bx+c,
由函数经过(-2,0),B(2,0),C(0,-1)三点可得:
,解得a=
,b=0,c=-1,
所以y=
x2-1;
(2)证明:设M(x1,y1),N(x2,y2),因为点M、N在抛物线上,
所以 y1=
-1,y2=
-1,所以
=4(y2+1);
又ON2=x22+y22=4(y2+1)+y22=(y2+2)2,所以ON=|2+y2|,
又因为y2为正,所以ON=2+y2,
设ON的中点E,分别过点N、E向直线l、作垂线,垂足为P、F,则EF=
=1+
,
所以ON=2EF,即ON的中点到直线l1的距离等于ON长度的一半,
所以以ON为直径的圆与l1相切;
(3)解:过点M作MH⊥NP交NP于点H,则MN2=MH2+NH2=(x2-x1)2+(y2-y1)2,
又y1=kx1,y2=kx2,所以(y2-y1)2=k2(x2-x1)2
所以MN2=(1+k2)(x2-x1)2;
又因为点M,N在y=kx的图象上又在抛物线上,
所以kx=
x2-1,即x2-4kx-4=0,所以x=
=2k±2
所以(x2-x1)2=16(1+k2)
所以MN2=16(1+k2)2,MN=4(1+k2).
证明:延长NP交l2于点Q,过点M作MS丄l2交l2于点S,
则MS+NQ=y1+2+y2+2=
-1+
-1+4=
(
+
)+2
又
+
=(x1+x2)2-2x1x2=16k2+8,
所以MS+NQ=4k2+2+2=4(1+k2)=MN,即M、N两点到l2距离之和等于线段MN的长.
由函数经过(-2,0),B(2,0),C(0,-1)三点可得:
|
| 1 |
| 4 |
所以y=
| 1 |
| 4 |
(2)证明:设M(x1,y1),N(x2,y2),因为点M、N在抛物线上,

所以 y1=
| 1 |
| 4 |
| x | 2 1 |
| 1 |
| 4 |
| x | 2 2 |
| x | 2 2 |
又ON2=x22+y22=4(y2+1)+y22=(y2+2)2,所以ON=|2+y2|,
又因为y2为正,所以ON=2+y2,
设ON的中点E,分别过点N、E向直线l、作垂线,垂足为P、F,则EF=
| OC+NP |
| 2 |
| y2 |
| 2 |
所以ON=2EF,即ON的中点到直线l1的距离等于ON长度的一半,
所以以ON为直径的圆与l1相切;
(3)解:过点M作MH⊥NP交NP于点H,则MN2=MH2+NH2=(x2-x1)2+(y2-y1)2,
又y1=kx1,y2=kx2,所以(y2-y1)2=k2(x2-x1)2
所以MN2=(1+k2)(x2-x1)2;
又因为点M,N在y=kx的图象上又在抛物线上,
所以kx=
| 1 |
| 4 |
4k±
| ||
| 2 |
| 1+k2 |
所以(x2-x1)2=16(1+k2)
所以MN2=16(1+k2)2,MN=4(1+k2).
证明:延长NP交l2于点Q,过点M作MS丄l2交l2于点S,
则MS+NQ=y1+2+y2+2=
| 1 |
| 4 |
| x | 2 1 |
| 1 |
| 4 |
| x | 2 2 |
| 1 |
| 4 |
| x | 2 1 |
| x | 2 2 |
又
| x | 2 1 |
| x | 2 2 |
所以MS+NQ=4k2+2+2=4(1+k2)=MN,即M、N两点到l2距离之和等于线段MN的长.
点评:本题考查待定系数法求函数解析式,考查根与系数的关系,梯形的中位线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
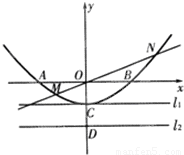
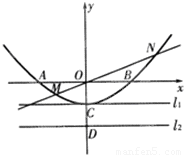
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式; 表示),并证明M、N两
表示),并证明M、N两
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D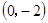 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线
.(1)求抛物线对应的二次函数的解析式;(2)求证:以ON为直径的圆与直线 表示),并证明M、N两点到直线
表示),并证明M、N两点到直线