题目内容
14．如图，指数函数的图象过点E（2，9），则图中阴影部分的面积等于（ ）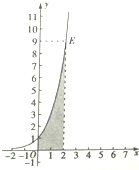
| A． | $\frac{8}{ln3}$ | B． | 8 | C． | $\frac{9}{ln3}$ | D． | 9 |
分析 根据指数函数y=ax的图象过点（2，9），确定函数的解析式，再用定积分表示阴影的面积，从而可求阴影的面积．
解答 解：∵指数函数y=ax的图象过点（2，9），
∴9=a2，
∴a=3，∴指数函数为y=3x，
∴阴影部分的面积等于${∫}_{0}^{2}$3xdx=$（\frac{1}{ln3}•{3}^{x}）{|}_{0}^{2}$=$\frac{8}{ln3}$
故选：A．
点评 本题考查指数函数的解析式，考查利用定积分求面积，解题的关键是确定被积函数．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
5．
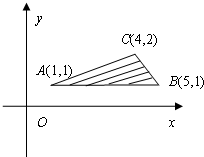在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）
在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
4．
执行如图所示的程序框图，输出的s的值为（ ）
执行如图所示的程序框图，输出的s的值为（ ）| A． | $\frac{9}{5}$ | B． | $\frac{7}{4}$ | C． | $\frac{11}{6}$ | D． | $\frac{4}{5}$ |