题目内容
对于任意15．实数x1，x2，max{x1，x2}表示x1，x2中较大的那个数，则当x∈R时，函数f（x）=max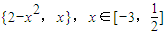
的最大值 ．
【答案】分析：根据新定义，已知x∈[-3，
]，分别求出函数2-x2和x的值域，求出最大值．
解答：解：∵实数x1，x2，max{x1，x2}表示x1，x2中较大的那个数，
∵x∈[-3，
]，
∴当x=0时2-x2有最大值为2，
∴f（x）=max{2-x2，x}=2，
故答案为2．
点评：此题是一道新定义题，考查了函数的最值及其几何意义，是道基础题．
]，分别求出函数2-x2和x的值域，求出最大值．解答：解：∵实数x1，x2，max{x1，x2}表示x1，x2中较大的那个数，
∵x∈[-3，
]，∴当x=0时2-x2有最大值为2，
∴f（x）=max{2-x2，x}=2，
故答案为2．
点评：此题是一道新定义题，考查了函数的最值及其几何意义，是道基础题．
练习册系列答案
相关题目
，则函数f(x)＝x2*[(6－x)*(2x＋15)]的最大值为
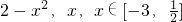的最大值________．