题目内容
F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.向量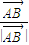 在向量
在向量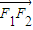 方向的投影是p.
方向的投影是p.(1)根据条件求出b和k满足的关系式;
(2)当
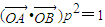 时,求直线l的方程;
时,求直线l的方程;(3)当
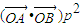 =m,且满足2≤m≤4时,求△AOB面积的取值范围.
=m,且满足2≤m≤4时,求△AOB面积的取值范围.
【答案】分析:(1)先利用条件求出圆O的方程,再利用圆心到直线的距离等于半径可得b和k满足的关系式;
(2)先把直线l的方程与双曲线方程联立求出A、B两点的坐标与b和k之间的等式,再利用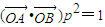 以及(1)的结论求出b和k进而求得直线l的方程;
以及(1)的结论求出b和k进而求得直线l的方程;
(3)用类似于(2)的方法求出之间的关系式,求出弦AB的长,再把△AOB面积整理成关于m的函数;利用函数的单调性求出△AOB面积的取值范围即可.
解答:解:(1)双曲线x2-y2=1的两个焦点分别是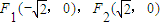 ,从而圆O的方程为x2+y2=2.
,从而圆O的方程为x2+y2=2.
由于直线y=kx+b与圆O相切,
所以有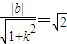 .
.
即b2=2(k2+1),(k≠±1)为所求.(3分)
(2)设A(x1,y1),B(x2,y2)
则由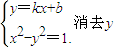 并整理得,(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1.
并整理得,(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1.
根据韦达定理,得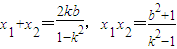 .(5分)
.(5分)
从而
=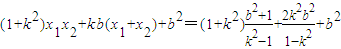 .
.
又由(1)知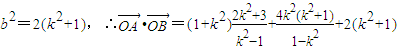 .
.
又由于 方向上的投影为p,
方向上的投影为p,
所以 .
.
即2k2+3-4k2+2k2-2=k2-1,(8分)
∴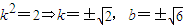
所以直线l的方程为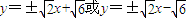 .(9分)
.(9分)
(3)类似于(2)可得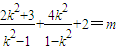 ,
,
即2k2+3-4k2+2k2-2=mk2-m,
∴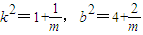 .(10分)
.(10分)
根据弦长公式,得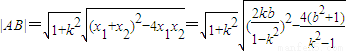 =
=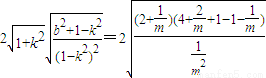
=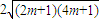 .
.
∵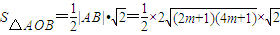
=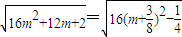
而2≤m≤4,
∴当m=2时,
当m=4时,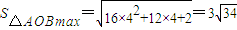
因此△AOB面积的取值范围是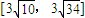 .(14分)
.(14分)
点评:本题是对函数,向量,抛物线以及圆的综合考查,由于知识点较多,是道难题.
(2)先把直线l的方程与双曲线方程联立求出A、B两点的坐标与b和k之间的等式,再利用
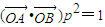 以及(1)的结论求出b和k进而求得直线l的方程;
以及(1)的结论求出b和k进而求得直线l的方程;(3)用类似于(2)的方法求出之间的关系式,求出弦AB的长,再把△AOB面积整理成关于m的函数;利用函数的单调性求出△AOB面积的取值范围即可.
解答:解:(1)双曲线x2-y2=1的两个焦点分别是
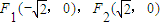 ,从而圆O的方程为x2+y2=2.
,从而圆O的方程为x2+y2=2.由于直线y=kx+b与圆O相切,
所以有
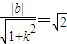 .
.即b2=2(k2+1),(k≠±1)为所求.(3分)
(2)设A(x1,y1),B(x2,y2)
则由
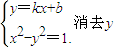 并整理得,(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1.
并整理得,(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1.根据韦达定理,得
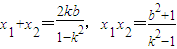 .(5分)
.(5分)从而

=
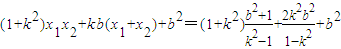 .
.又由(1)知
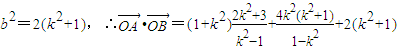 .
.又由于
 方向上的投影为p,
方向上的投影为p,所以
 .
.即2k2+3-4k2+2k2-2=k2-1,(8分)
∴
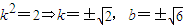
所以直线l的方程为
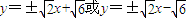 .(9分)
.(9分)(3)类似于(2)可得
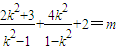 ,
,即2k2+3-4k2+2k2-2=mk2-m,
∴
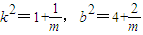 .(10分)
.(10分)根据弦长公式,得
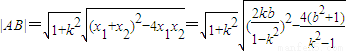 =
=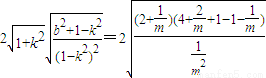
=
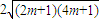 .
.∵
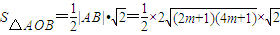
=
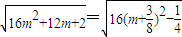
而2≤m≤4,
∴当m=2时,

当m=4时,
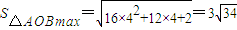
因此△AOB面积的取值范围是
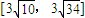 .(14分)
.(14分)点评:本题是对函数,向量,抛物线以及圆的综合考查,由于知识点较多,是道难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目