题目内容
已知函数![]() ,设
,设![]() 。
。
(I)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与函数
的图象与函数![]() 的图象恰有四个不同的交点?若存在,求出实数
的图象恰有四个不同的交点?若存在,求出实数![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
解析:(I)![]()
![]() (2分)
(2分)
因为![]() ,由
,由![]() ,所以
,所以![]() 在
在![]() 上单调递增。
上单调递增。
由![]() ,所以
,所以![]() 在
在![]() 上单调递减。
上单调递减。
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() (6分)
(6分)
(Ⅱ)若![]() 的图像与
的图像与![]() 的图像恰有四个不同的交点。
的图像恰有四个不同的交点。
即![]() 有四个不同的根,亦即
有四个不同的根,亦即![]() 有四个不同的根。
有四个不同的根。
令![]()
则![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
当![]() 变化时,
变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
| + |
| + |
|
|
|
|
|
|
由表格知;![]()
画出草图和验证可知![]()
所以当![]() 时,
时,![]() 与
与![]() 恰有四个不同的交点。
恰有四个不同的交点。

练习册系列答案
相关题目
 (
( ,
,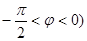 图像上一个最低点
图像上一个最低点 .
. 的解析式;
的解析式; 求
求 的值.
的值. 且存在
且存在 使
使
 是R上的单调增函数;
是R上的单调增函数; 其中
其中 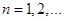
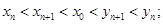

 。
。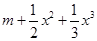 。
。 时,设函数f(x)的导函数为
时,设函数f(x)的导函数为 ,令Tn=
,令Tn=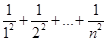 ,证明:Tn
,证明:Tn 1
1 ,设
,设 。
。 的单调区间;
的单调区间; ,使得函数
,使得函数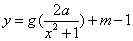 的图象与函数
的图象与函数 的图象恰有四个不同的交点?若存在,求出实数
的图象恰有四个不同的交点?若存在,求出实数