题目内容
巳知等比数列{an}满足an>0,n=1,2…,且a5•a2n-5=22n(n≥3),则当n≥1时,㏒2α1+㏒2α3+…+㏒2α2n-1=______.
∵a5•a2n-5=22n=an2,an>0,
∴an=2n,
∴log2a1+log2a3+…+log2a2n-1=log2(a1a3…a2n-1)=log221+3+…+(2n-1)=log22n2=n2.
故答案为:n2
∴an=2n,
∴log2a1+log2a3+…+log2a2n-1=log2(a1a3…a2n-1)=log221+3+…+(2n-1)=log22n2=n2.
故答案为:n2

练习册系列答案
相关题目
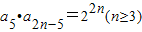 ,则当n≥1时,㏒2α1+㏒2α3+…+㏒2α2n-1= .
,则当n≥1时,㏒2α1+㏒2α3+…+㏒2α2n-1= .