题目内容
平面内到定点(1,0)和到定点(4,0)的距离的比为 的点的轨迹为曲线M,直线l与曲线M相交于A,B两点,若在曲线M上存在点C,使
的点的轨迹为曲线M,直线l与曲线M相交于A,B两点,若在曲线M上存在点C,使 ,且
,且 ,求直线l的斜率及对应的点C的坐标.
,求直线l的斜率及对应的点C的坐标.
【答案】分析:设曲线C上的任意一点P(x,y),利用平面内到定点(1,0)和到定点(4,0)的距离的比为 ,可得
,可得 ,从而可求曲线C的方程;利用
,从而可求曲线C的方程;利用 ,且
,且 ,可得
,可得 ,
, ,从而可求直线l的斜率,设C(x,y),利用
,从而可求直线l的斜率,设C(x,y),利用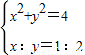 ,可求对应的点C的坐标为.
,可求对应的点C的坐标为.
解答:解:设曲线C上的任意一点P(x,y),则 ,
,
化简可得曲线C的方程为x2+y2=4.…(4分)
∵ ,且
,且
∴ ,
,
∵
∴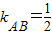 …(8分)
…(8分)
设C(x,y),由 ,解得
,解得 或
或
∴直线l的斜率为 ,对应的点C的坐标为
,对应的点C的坐标为 或
或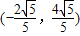 .…(12分)
.…(12分)
点评:本题考查轨迹方程的求法,考查向量知识的运用,考查直线的斜率,解题的关键是掌握轨迹方程的一般求法.
 ,可得
,可得 ,从而可求曲线C的方程;利用
,从而可求曲线C的方程;利用 ,且
,且 ,可得
,可得 ,
, ,从而可求直线l的斜率,设C(x,y),利用
,从而可求直线l的斜率,设C(x,y),利用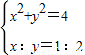 ,可求对应的点C的坐标为.
,可求对应的点C的坐标为.解答:解:设曲线C上的任意一点P(x,y),则
 ,
,化简可得曲线C的方程为x2+y2=4.…(4分)
∵
 ,且
,且
∴
 ,
,
∵

∴
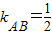 …(8分)
…(8分)设C(x,y),由
 ,解得
,解得 或
或
∴直线l的斜率为
 ,对应的点C的坐标为
,对应的点C的坐标为 或
或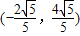 .…(12分)
.…(12分)点评:本题考查轨迹方程的求法,考查向量知识的运用,考查直线的斜率,解题的关键是掌握轨迹方程的一般求法.

练习册系列答案
相关题目
 的点的轨迹为曲线M,直线l与曲线M相交于A,B两点,若在曲线M上存在点C,使
的点的轨迹为曲线M,直线l与曲线M相交于A,B两点,若在曲线M上存在点C,使 ,且
,且 =(-1,2),求直线l的斜率及对应的点C的坐标。
=(-1,2),求直线l的斜率及对应的点C的坐标。