题目内容
某人睡午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间不多于15分钟的概率为
A.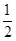 | B. | C. | D.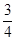 |
B
解析试题分析:整点报时,整点之间共六十分钟,等待时间不多于15分钟,所以他等待时间不多于15分钟的概率为 ,故选B.
,故选B.
考点:本题主要考查几何概型概率的计算。
点评:简单题,几何概型概率的计算,关键是弄清两个“几何度量”,再求比值。

练习册系列答案
相关题目
已知 , 若
, 若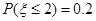 , 则
, 则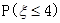 =( )
=( )
| A.0.2 | B.0.3 | C.0.7 | D.0.8 |
将一枚质地均匀的硬币连掷4次,出现“至少两次正面向上”的概率为
A. | B. | C. | D. |
下列说法正确的个数是
(1)线性回归方程 必过
必过
(2)在一个 列联表中,由计算得
列联表中,由计算得 =4.235,则有95%的把握确认这两个变量间没有关系
=4.235,则有95%的把握确认这两个变量间没有关系
(3)复数
(4)若随机变量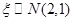 ,且p(
,且p( <4)=p,则p(0<
<4)=p,则p(0< <2)=2p-1
<2)=2p-1
| A.1 | B.2 | C.3 | D. 4 |
已知函数 ,其中
,其中 ,则使得
,则使得 在
在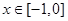 上有解的概率为( )
上有解的概率为( )
A. | B. | C.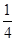 | D. |
在区间 上任取一个实数
上任取一个实数 ,则
,则 的概率等于
的概率等于
A. | B. | C. | D. |
从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是( )
| A.1 | B. | C. | D. |








