题目内容
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的结果如下:
(1)求表中a,b的值
(2)若以上表频率作为概率,且每天的销售量相互独立.
(3)①求5天中该种商品恰有2天销售量为1.5吨的概率;②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和(单位:千元),求X的分布列和期望.
| 日销售量 | 1 | 1.5 | 2 |
| 频数 | 10 | 25 | 15 |
| 频率 | 0.2 | a | b |
(2)若以上表频率作为概率,且每天的销售量相互独立.
(3)①求5天中该种商品恰有2天销售量为1.5吨的概率;②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和(单位:千元),求X的分布列和期望.
分析:(1)利用频率等于频数除以样本容量,求出样本容量,再求出表中的a,b.
(2)①利用二项分布的概率公式求出5天中该种商品恰好有2天的销售量为1.5吨的概率.
②写出ξ可取得值,利用相互独立事件的概率公式求出ξ取每一个值的概率.列出分布列,求得期望.
(2)①利用二项分布的概率公式求出5天中该种商品恰好有2天的销售量为1.5吨的概率.
②写出ξ可取得值,利用相互独立事件的概率公式求出ξ取每一个值的概率.列出分布列,求得期望.
解答:解:(1)∵
=50∴a=
=0.5,b=
=0.3
(2)①依题意,随机选取一天,销售量为1.5吨的概率p=0.5
设5天中该种商品有X天的销售量为1.5吨,则X~B(5,0.5)
P(X=2)=C52×0.52×(1-0.5)3=0.3125
②ξ的可能取值为4,5,6,7,8,则
p(ξ=4)=0.22=0.04
p(ξ=5)═2×0.2×0.5=0.2
p(ξ=6)═0.52+2×0.2×0.3=0.37
p(ξ=7)═2×0.3×0.5=0.3
p(ξ=8)=0.32=0.09
所有C的分布列为:
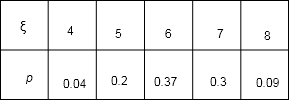
Eξ=4×0.04+5×0.2+6×0.37+7×0.3+8×0.09=6.2.
| 10 |
| 0.2 |
| 25 |
| 50 |
| 15 |
| 50 |
(2)①依题意,随机选取一天,销售量为1.5吨的概率p=0.5
设5天中该种商品有X天的销售量为1.5吨,则X~B(5,0.5)
P(X=2)=C52×0.52×(1-0.5)3=0.3125
②ξ的可能取值为4,5,6,7,8,则
p(ξ=4)=0.22=0.04
p(ξ=5)═2×0.2×0.5=0.2
p(ξ=6)═0.52+2×0.2×0.3=0.37
p(ξ=7)═2×0.3×0.5=0.3
p(ξ=8)=0.32=0.09
所有C的分布列为:

Eξ=4×0.04+5×0.2+6×0.37+7×0.3+8×0.09=6.2.
点评:本题主要考查随机事件、互斥事件、相互独立事件等概率知识、考查离散型随机变量的分布列和期望等基础知识,考查运用概率与统计知识解决实际问题的能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
某批发市场对某种商品日销售量(单位吨)进行统计,最近50天的统计结果如图.
(1)计算这50天的日平均销售量;
(2)若以频率为概率,其每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)若以频率为概率,其每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,ξ表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求ξ的分布列和数学期望.
| 周销售量 | 2 | 3 | 4 |
| 频数 | 20 | 50 | 30 |
(2)已知每吨该商品的销售利润为2千元,ξ表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求ξ的分布列和数学期望.