题目内容
抛物线y =4x的焦点坐标为
=4x的焦点坐标为
| A.(2,0) | B.(1,0) | C.(0,-4) | D.(-2,0) |
B
解析考点:抛物线的简单性质.
分析:先确定焦点位置,即在x轴正半轴,再求出P的值,可得到焦点坐标.
解:∵抛物线y2=4x是焦点在x轴正半轴的标准方程,
p=2∴焦点坐标为:(1,0)
故答案为:B

练习册系列答案
相关题目
顶点在原点,且过点 的抛物线的标准方程是( )
的抛物线的标准方程是( )
A. | B. |
C. 或 或 | D. 或 或 |
与椭圆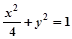 共焦点且过点P(2,1)的双曲线方程是 ( )
共焦点且过点P(2,1)的双曲线方程是 ( )
A.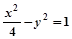 | B.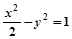 | C.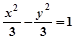 | D.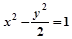 |
曲线y2=4x关于直线x=2对称的曲线方程是( )
| A.y2=8-4x | B.y2=4x-8 |
| C.y2=16-4x | D.y2=4x-16 |
抛物线 的焦点到准线的距离是( )高( )^ ((考#资*源^网
的焦点到准线的距离是( )高( )^ ((考#资*源^网
| A.1 | B.2 | C.4 | D.8 |
设定点 与抛物线
与抛物线 上的点
上的点 的距离为
的距离为 ,
, 到抛物线焦点F的距离为
到抛物线焦点F的距离为 ,则
,则 取最小值时,
取最小值时, 点的坐标为( ).
点的坐标为( ).
A. | B. | C. | D.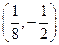 |
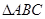 中,
中, ,
,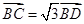 , A
, A ,则
,则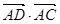 的值为( ) B D C
的值为( ) B D C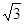
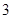
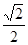
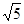

 :
: ,以抛物线
,以抛物线 的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为
的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为  A.
A. B.
B.  C.
C.  D.
D. 
 的焦距是( )
的焦距是( )
