题目内容
已知函数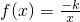 在(0,+∞)上单调递增,则实数k的取值范围是
在(0,+∞)上单调递增,则实数k的取值范围是
- A.(-∞,0)
- B.(0,+∞)
- C.(1,+∞)
- D.(-∞,1)
B
分析:根据反比例函数f(x)= 在(0,+∞)的单调性,可以得出f(x)=-
在(0,+∞)的单调性,可以得出f(x)=- 在(0,+∞)上的单调性,进而再根据f(x)=
在(0,+∞)上的单调性,进而再根据f(x)=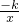 =k
=k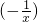 在(0,+∞)上是单调递增的求出k的取值范围.
在(0,+∞)上是单调递增的求出k的取值范围.
解答:因为反比例函数f(x)= 在(0,+∞)的单调递减,所以函数f(x)=-
在(0,+∞)的单调递减,所以函数f(x)=- 在(0,+∞)上的单调递增,
在(0,+∞)上的单调递增,
又因为函数f(x)=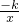 =k
=k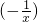 在(0,+∞)上单调递增,所以,k>0.
在(0,+∞)上单调递增,所以,k>0.
故选B
点评:本题考查的是反比例函数的单调性的有关问题.对于反比例函数要注意其定义域的不连续性,并且在其定义域的每一区间都是单调递减的.
分析:根据反比例函数f(x)=
 在(0,+∞)的单调性,可以得出f(x)=-
在(0,+∞)的单调性,可以得出f(x)=- 在(0,+∞)上的单调性,进而再根据f(x)=
在(0,+∞)上的单调性,进而再根据f(x)=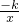 =k
=k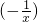 在(0,+∞)上是单调递增的求出k的取值范围.
在(0,+∞)上是单调递增的求出k的取值范围.解答:因为反比例函数f(x)=
 在(0,+∞)的单调递减,所以函数f(x)=-
在(0,+∞)的单调递减,所以函数f(x)=- 在(0,+∞)上的单调递增,
在(0,+∞)上的单调递增,又因为函数f(x)=
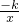 =k
=k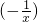 在(0,+∞)上单调递增,所以,k>0.
在(0,+∞)上单调递增,所以,k>0.故选B
点评:本题考查的是反比例函数的单调性的有关问题.对于反比例函数要注意其定义域的不连续性,并且在其定义域的每一区间都是单调递减的.

练习册系列答案
相关题目
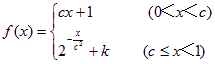 在区间(0,1)内连续,且
在区间(0,1)内连续,且 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.

 在区间[0,1]上的最小值为0,则a的值为
。
在区间[0,1]上的最小值为0,则a的值为
。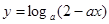 在[0,1]上是减函数,则a的取值范围是
.
在[0,1]上是减函数,则a的取值范围是
.