题目内容
通常情况下,同一地区一天的温度随时间变化的曲线接近于函数y=Asin(ωx+φ)+b的图象.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为14°C;最低温度出现在凌晨2时,最低温度为零下2°C.
(Ⅰ)请推理荆门地区该时段的温度函数y=Asin(ωt+φ)+b(A>0,ω>0,|φ|<π,t∈[0,24))的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于10°C,教室就要开空调,请问届时学校后勤应该送电吗?
(Ⅰ)请推理荆门地区该时段的温度函数y=Asin(ωt+φ)+b(A>0,ω>0,|φ|<π,t∈[0,24))的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于10°C,教室就要开空调,请问届时学校后勤应该送电吗?
分析:(I)根据函数最大、最小值的和与差,算出A=8且b=6,由函数的周期为24算出ω=
,再根据当x=2时函数有最小值,算出φ=-
即可得到所求温度函数的表达式;
(II)算出函数当x=9时的函数值f(9),利用特殊三角函数值算出f(9)<10,得到此时满足开空调的条件,所以应该开空调.
| π |
| 12 |
| 2π |
| 3 |
(II)算出函数当x=9时的函数值f(9),利用特殊三角函数值算出f(9)<10,得到此时满足开空调的条件,所以应该开空调.
解答:解:(I)∵最高温度为14°C,最低温度为零下2°C.
∴A=
[14-(-2)]=8,b=
[14+(-2)]=6,
∵函数的周期T=24,∴ω=
=
由
•2+φ=-
+2kπ,|φ|<π,可得φ=-
(5分)
∴函数表达式为y=8sin(
x-
)+6(6分);
(II)当x=9时,y=8sin(
•9-
)+6=8sin
+6(8分)
∵sin
<sin
,∴y=8sin
+6<8sin
+6=10,(11分)
温度低于10°C,满足开空调的条件,所以应该开空调.(12分)
∴A=
| 1 |
| 2 |
| 1 |
| 2 |
∵函数的周期T=24,∴ω=
| 2π |
| 24 |
| π |
| 12 |
由
| π |
| 12 |
| π |
| 2 |
| 2π |
| 3 |
∴函数表达式为y=8sin(
| π |
| 12 |
| 2π |
| 3 |
(II)当x=9时,y=8sin(
| π |
| 12 |
| 2π |
| 3 |
| π |
| 12 |
∵sin
| π |
| 12 |
| π |
| 6 |
| π |
| 12 |
| π |
| 6 |
温度低于10°C,满足开空调的条件,所以应该开空调.(12分)
点评:本题给出实际应用问题,求函数表达式并确定某个时刻能否开空调.着重考查了三角函数的图象与性质和三角函数在实际生活中的应用等知识,属于中档题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
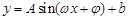 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为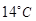 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下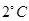 .
.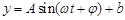
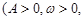
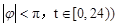 的表达式;
的表达式;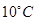 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?