题目内容
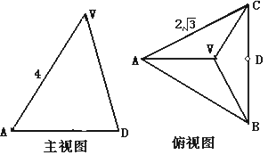
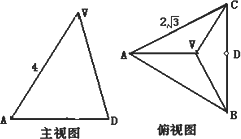
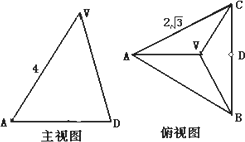
正三棱锥V－ABC的底面边长为2，侧棱长为3，过底面AB边的截面交侧棱VC于P点．
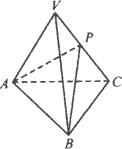
(1)若P为VC的中点，求
；
(2)若P为动点，P∈VC，求△PAB面积的最小值．
答案：
解析：
解析：
|
解：(1)作VO⊥底面ABC于O，连CO，并延长交AB于D，连VD， ∴AB⊥平面VCD，平面ABC⊥平面VCD，作PE⊥CD于E． ∴PE⊥平面ABC．又P为VC中点，
∴ (2)设PC=x， ∴ 故当 |
，
；
；
，由余弦定理
，
时，
面积最小，最小值为
．
练习册系列答案
阅读快车系列答案
相关题目
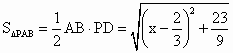，高为2，则侧棱与底面所成角的大小为
a2，＋∞)
a2，＋∞)
a2，＋∞)
，则该三棱锥的左视图的面积；
，则该三棱锥的左视图的面积；
，则该三棱锥的左视图的面积；
