题目内容
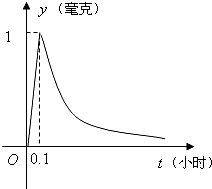 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(| 1 | 16 |
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么,药物释放开始,至少需要经过
分析:(1)当0≤t≤0.1时,可设y=kt,把点(0.1,1)代入直线方程求得k,得到直线方程;当t>0.1时,把点(0.1,1)代入y=(
)t-a求得a,曲线方程可得.最后综合可得答案.
(2)根据题意可知y≤0.25,把(1)中求得的函数关系式,代入即可求得t的范围.
| 1 |
| 16 |
(2)根据题意可知y≤0.25,把(1)中求得的函数关系式,代入即可求得t的范围.
解答:解:(I)由题意和图示,当0≤t≤0.1时,可设y=kt(k为待定系数),由于点(0.1,1)在直线上,∴k=10;
同理,当t>0.1时,可得1=(
)0.1-a?0.1-a=0?a=
(II)由题意可得y≤0.25=
,
即得
或
?0≤t≤
或t≥0.6,
由题意至少需要经过0.6小时后,学生才能回到教室.
同理,当t>0.1时,可得1=(
| 1 |
| 16 |
| 1 |
| 10 |
(II)由题意可得y≤0.25=
| 1 |
| 4 |
即得
|
|
| 1 |
| 40 |
由题意至少需要经过0.6小时后,学生才能回到教室.
点评:本题考查函数、不等式的实际应用,以及识图和理解能力.易错点:只单纯解不等式,而忽略题意,在(II)中填写了其他错误答案.

练习册系列答案
相关题目
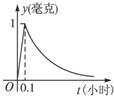 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=( 为了预防流感,某学校对教室用药物消毒法进行消毒,已知从药物投放开始,室内每立方米空气含药量y(单位:毫克)与时间t(单位:小时)的函数关系为:药物释放的过程中,y=kt(k为常数);药物释放完毕后,
为了预防流感,某学校对教室用药物消毒法进行消毒,已知从药物投放开始,室内每立方米空气含药量y(单位:毫克)与时间t(单位:小时)的函数关系为:药物释放的过程中,y=kt(k为常数);药物释放完毕后, 为了预防流感,某学校对教室用药熏消毒法进行消毒.如图所示,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,室内每立方米空气中的含药量y(毫克)与时间t(小时)的函数关系式为
为了预防流感,某学校对教室用药熏消毒法进行消毒.如图所示,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,室内每立方米空气中的含药量y(毫克)与时间t(小时)的函数关系式为 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=(