题目内容
某抛物线型拱桥的跨度是20米,拱高4米.在建桥时每隔4米需要一支柱支撑,其中最长的支柱是多少米?
分析:本题利用解析法解决.先建立适当坐标系,设抛物线方程为x2=-2py(p>0),把点B(10,-4)代入抛物线方程,求得p,得到抛物线方程,进而把x=2代入抛物线方程求得y,可得最高支柱的高度.
解答: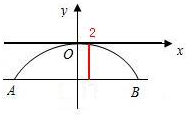 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,
设抛物线方程为x2=-2py(p>0),
∵过定点B(10,-4),
代入x2=-2py,得p=
.
∴x2=-25y.
当x=2时,y=
,
∴最长支柱长为4-|y|=4-
=3.84(m),
故在建桥时每隔4米需要一支柱支撑,其中最长的支柱是:3.84米.
 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,设抛物线方程为x2=-2py(p>0),
∵过定点B(10,-4),
代入x2=-2py,得p=
| 25 |
| 2 |
∴x2=-25y.
当x=2时,y=
| -4 |
| 25 |
∴最长支柱长为4-|y|=4-
| 4 |
| 25 |
故在建桥时每隔4米需要一支柱支撑,其中最长的支柱是:3.84米.
点评:本题主要考查了抛物线的应用和抛物线的标准方程.解应用题需要把文字语言转化为形式化数学语言.本题就是要利用解析法解决,介入一个抛物线方程,利用抛物线的性质来解决问题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目