题目内容
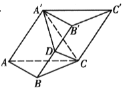
【题目】在△ABC中，∠C＝90°，AB＝2，
，D为AC上的一点（不含端点），将△BCD沿直线BD折起，使点C在平面ABD上的射影O在线段AB上，则线段OB的取值范围是（ ）
A.（
，1）B.（，
）C.（，1）D.（0，）
【答案】A
【解析】
由题意，OC⊥平面ABD，根据三余弦定理，线线角的余弦值等于线面角的余弦值与射影角余弦值的积，从而求解.
由题意，OC⊥平面ABD，
如图：
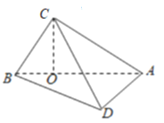
设∠CBD＝θ，∠CBO＝θ1，则∠ABD＝60°-θ；则cosθ＝cosθ1×cos（60°﹣θ）
所以cosθ1
，
∵θ∈（30°，60°）；
∴OB＝cosθ1∈（
，1）．
故选：A．
本题考查△ABC的折叠和三余弦定理（最小角定理），要求熟悉余弦定理，属于中档题．
【题目】近年来，某市为了促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
（Ⅰ）试估计厨余垃圾投放正确的概率
（Ⅱ）试估计生活垃圾投放错误的概率
（Ⅲ）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0，a+b+c=600.当数据a,b,c,的方差
最大时，写出a,b,c的值（结论不要求证明），并求此时的值．
（注：
，其中
为数据
的平均数）
【题目】微信运动，是由腾讯开发的一个类似计步数据库的公众账号．用户可以通过关注微信运动公众号查看自己每天行走的步数，同时也可以和其他用户进行运动量的
或点赞．微信运动公众号为了解用户的一些情况，在微信运动用户中随机抽取了100名用户，统计了他们某一天的步数，数据整理如下：
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
（1）根据表中数据，在如图所示的坐标平面中作出其频率分布直方图，并在纵轴上标明各小长方形的高；
（2）利用分层抽样的方法，从步数在
（万步）中抽取7人，再从这7人中随机抽取2人，求步数在
（万步）的人恰有1人的概率；
（3）这100名用户中，
的用户为男生，这些男生的步数超过1.2万步的人为20人，是否有
的把握认为运动步数超过1.2万步与性别有关？
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
