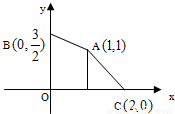题目内容
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是( )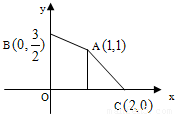
A.a<-1
B.a>-

C.-1<a<-

D.-1≤a≤-

【答案】分析:先根据约束条件画出可行域,再利用几何意义求最值,z=ax-y表示直线在y轴上的截距的相反数,a表示直线的斜率,只需求出a取值在什么范围时,直线z=ax-y在y轴上的截距最优解在点A处即可.
解答:解:由可行域可知,直线AC的斜率= ,
,
直线AB的斜率=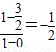 ,
,
当直线z=ax-y的斜率介于AC与AB之间时,
A(1,1)是该目标函数z=ax-y的唯一最优解,
所以-1≤a≤- ,
,
故选D.
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于基础题.解答的关键是根据所给区域得到关于直线斜率的不等关系,这是数学中的数形结合的思想方法.
解答:解:由可行域可知,直线AC的斜率=
 ,
,直线AB的斜率=
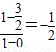 ,
,当直线z=ax-y的斜率介于AC与AB之间时,
A(1,1)是该目标函数z=ax-y的唯一最优解,
所以-1≤a≤-
 ,
,故选D.
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于基础题.解答的关键是根据所给区域得到关于直线斜率的不等关系,这是数学中的数形结合的思想方法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
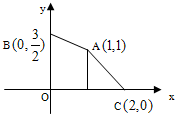 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是( )
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是( )| A、a<-1 | ||
B、a>-
| ||
C、-1<a<-
| ||
D、-1≤a≤-
|