题目内容
(上海卷理20)设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线,记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点
⑴已知a=1,b=2,p=2,求点Q的坐标.
⑵已知点P(a,b)(ab≠0)在椭圆+y2=1上,p=,求证:点Q落在双曲线4x2-4y2=1上.
⑶已知动点P(a,b)满足ab≠0,p=,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由.
【解析】(1)当![]() 时,
时,
解方程组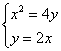 得
得![]() 即点
即点![]() 的坐标为
的坐标为![]() ……3分
……3分
(2)【证明】由方程组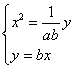 得
得![]() 即点
即点![]() 的坐标为
的坐标为![]() …5分
…5分
![]() 时椭圆上的点,即
时椭圆上的点,即![]()
![]() ,
,
因此点![]() 落在双曲线
落在双曲线![]() 上 ……8分
上 ……8分
(3)设![]() 所在的抛物线方程为
所在的抛物线方程为![]() ……10分
……10分
将![]() 代入方程,得
代入方程,得![]() ,即
,即![]() ……12分
……12分
当![]() 时,
时,![]() ,此时点
,此时点![]() 的轨迹落在抛物线上;
的轨迹落在抛物线上;
当![]() 时,
时,![]() ,此时点
,此时点![]() 的轨迹落在圆上;
的轨迹落在圆上;
当![]() 时,
时, ,此时点
,此时点![]() 的轨迹落在椭圆上;
的轨迹落在椭圆上;
当![]() 时
时 ,此时点
,此时点![]() 的轨迹落在双曲线上; ……16分
的轨迹落在双曲线上; ……16分

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目