题目内容
已知AB=BC=CD，且线段BC是AB与CD的公垂线段，若AB与CD成60°角，则异面直线BC与AD所成的角为（ ）
| A、45° | B、60° | C、90° | D、45°或60° |
分析：建立如图的空间坐标系，∠ABY=60°或120，令AB=BC=CD=2，得出各点的坐标，求出BC与AD的坐标，即得两直线的方向向量，利用数量积公式求出两者的夹角即可
解答：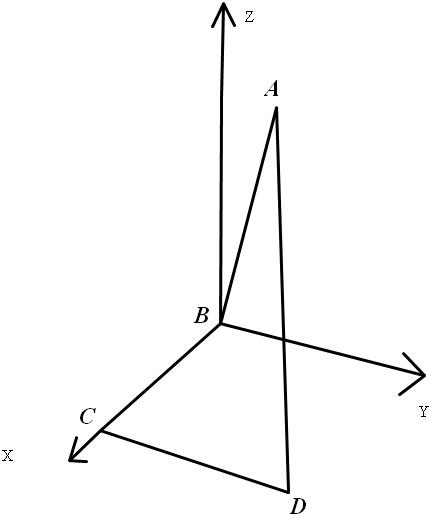
解：建立如图的空间坐标系，不妨令∠ABY=60°，令AB=BC=CD=2，得出各点的坐标分别为，B（0，0，0），C（2，0，0），D（2，2，0），A（0，1，
）
故
=（2，0，0），
=（2，1，-
）
故两直线的夹角的余弦是
=
=
故两直线所成角为45°
若∠ABY=120°时，同理可求得夹角的余弦值为
，可得两直线所成角为60°
综上两直线所成角为45°或60°
故选D
解：建立如图的空间坐标系，不妨令∠ABY=60°，令AB=BC=CD=2，得出各点的坐标分别为，B（0，0，0），C（2，0，0），D（2，2，0），A（0，1，| 3 |
故
| BC |
| AD |
| 3 |
故两直线的夹角的余弦是
| ||||
|
|
| 4 | ||
2×2
|
| ||
| 2 |
故两直线所成角为45°
若∠ABY=120°时，同理可求得夹角的余弦值为
| 1 |
| 2 |
综上两直线所成角为45°或60°
故选D
点评：本题考查求异面直线所成的角，求本题的关键是建立起符合题意的坐标系，求出两直线的方向向量，并利用数量积公式求出两直线夹角的余弦或其绝对值，解题时要注意两直线夹角的范围与两向量夹角范围的不同．
练习册系列答案
相关题目