题目内容
已知 、
、 ,椭圆C的方程为
,椭圆C的方程为 ,
, 、
、 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设 为椭圆C上一点,存在以
为椭圆C上一点,存在以 为圆心的
为圆心的 与
与 外切、与
外切、与 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作斜率为
作斜率为 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与 轴相交于点D,若
轴相交于点D,若
 求
求 的值;
的值;
(Ⅲ)已知真命题:“如果点T( )在椭圆
)在椭圆 上,那么过点T
上,那么过点T
的椭圆的切线方程为 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
【答案】
本题主要考查直线、圆、椭圆等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想
解:(Ⅰ)依题意可知, P与
P与
 外切、
外切、
 内切. 设
内切. 设 P的半径为
P的半径为 ,则
,则
 -----------------------------------2分
-----------------------------------2分

 , 2
, 2 =4,2
=4,2 =
= =2
=2

 =2,c=1 , 椭圆C的方程为
=2,c=1 , 椭圆C的方程为 +
+ =1 ------------------------4分
=1 ------------------------4分
(Ⅱ)直线AB:y=k(x-1),由



 ,令A
,令A ,则
,则 ,
,
 , ------------------------------------6分
, ------------------------------------6分
∵
∴ ,
,
∵2= ,
, ,
------------------------------------8分
,
------------------------------------8分
2+
=
=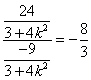 , ∴
, ∴ .
-----------------------10分
.
-----------------------10分
(Ⅲ)设Q( ),M(
),M( ),N(
),N( )
)
则切线QM:
切线QN: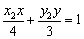
∴  ∴M、N在直线
∴M、N在直线 上
上
∴ 直线MN: ------------------------------------12分
------------------------------------12分
又
∴直线MN必过定点( ). ------------------------------------13分
). ------------------------------------13分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
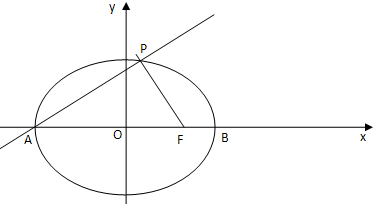 已知椭圆C的方程是
已知椭圆C的方程是