题目内容
已知命题A：若x＞1，则x+| 4 |
| x-1 |
| 3 |
| 2x |
分析：根据命题“若p则q”的逆否命题为“若￢q则￢p”及命题否定时逻辑连接词“且”与“或”要互化，易于写出命题A的逆否命题；
根据互为逆否命题的两命题真假性相同的特点，要判断命题A的逆否命题的真假，可判断命题A的真假，因为该命题更易于判断（利于基本不等式a+b≥2
即可）．
根据互为逆否命题的两命题真假性相同的特点，要判断命题A的逆否命题的真假，可判断命题A的真假，因为该命题更易于判断（利于基本不等式a+b≥2
| ab |
解答：解：命题A的逆否命题是“若x+
＜5或8-6x-
＞2，则x≤1成立”；
若x＞1，则x+
=x-1+
+1≥2×2+1=5且8-6x-
=8-（6x+
）≤8-2×3=2，
所以命题A为真命题，则其逆否命题也是真命题．
故答案为：“若x+
＜5或8-6x-
＞2，则x≤1成立”与“真命题”．
| 4 |
| x-1 |
| 3 |
| 2x |
若x＞1，则x+
| 4 |
| x-1 |
| 4 |
| x-1 |
| 3 |
| 2x |
| 3 |
| 2x |
所以命题A为真命题，则其逆否命题也是真命题．
故答案为：“若x+
| 4 |
| x-1 |
| 3 |
| 2x |
点评：本题考查四种命题的形式关系及逆否命题的真假关系，同时考查基本不等式的灵活运用．
练习册系列答案
备战中考寒假系列答案
相关题目
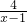≥5且8-6x-
≤2成立．命题A的逆否命题是________；该逆否命题是________．（填“真命题”或“假命题”）
≥5且8-6x-
≤2成立．命题A的逆否命题是 ；该逆否命题是 ．（填“真命题”或“假命题”）