题目内容
求证:(1)n≥0,试用分析法证明,| n+2 |
| n+1 |
| n+1 |
| n |
(2)当a、b、c为正数时,(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
相等的非零实数.用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
分析:(1)要证
-
<
-
成立,即证
+
>2
,即证 (
+
)2>(2
)2,即证n+1>
,即证 (n+1)2>n2+2n,即证1>0.
(2)假设三个方程中都没有两个相异实根,则他们的判别式都小于0,相加可得(a-b)2+(b-c)2+(c-a)2≤0 ①,
由题意a、b、c互不相等,可得①式不能成立,矛盾.
| n+2 |
| n+1 |
| n+1 |
| n |
| n+2 |
| n |
| n+1 |
| n+2 |
| n |
| n+1 |
| n2+2n |
(2)假设三个方程中都没有两个相异实根,则他们的判别式都小于0,相加可得(a-b)2+(b-c)2+(c-a)2≤0 ①,
由题意a、b、c互不相等,可得①式不能成立,矛盾.
解答:证明:(1)要证
-
<
-
成立,即证
+
>2
,
即证 (
+
)2>(2
)2,即证n+1>
,即证 (n+1)2>n2+2n,即n2+2n+1>n2+2n,
即证1>0,而1>0 显然成立,所以原命题成立.
(2)证明:假设三个方程中都没有两个相异实根,则△1=4b2-4ac≤0,△2=4c2-4ab≤0,
△3=4a2-4bc≤0. 相加有 a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.①由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
| n+2 |
| n+1 |
| n+1 |
| n |
| n+2 |
| n |
| n+1 |
即证 (
| n+2 |
| n |
| n+1 |
| n2+2n |
即证1>0,而1>0 显然成立,所以原命题成立.
(2)证明:假设三个方程中都没有两个相异实根,则△1=4b2-4ac≤0,△2=4c2-4ab≤0,
△3=4a2-4bc≤0. 相加有 a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.①由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
点评:本题考查用分析法证明不等式,用反证法证明不等式,用反证法证明不等式时,推出矛盾,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

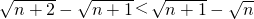 ,
, +
+ +
+ )≥9.
)≥9.