题目内容
设![]() 是偶函数,且当
是偶函数,且当![]() 时,
时,![]() .
.
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的表达式;
的表达式;
解: (1)当![]() 时,
时,![]()
同理,当![]() 时,
时,![]() ,
,
所以,当![]() 时,
时,![]() 的解析式为
的解析式为![]()
(2)因为![]() 是偶函数,所以它在区间
是偶函数,所以它在区间![]() 上的最大值即为它在区间
上的最大值即为它在区间![]() 上的最大值,
上的最大值,
①当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() .
.
②当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 与
与![]() 上单调递减,
上单调递减,
所以此时只需比较![]() 与
与![]() 的大小.
的大小.
(A)当![]() 时,
时, ![]() ≥
≥![]() ,所以
,所以![]()
(B)当![]() 时,
时, ![]() <
<![]() ,所以
,所以![]()
③当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() <
<![]() ,所以
,所以![]()
综上所述, 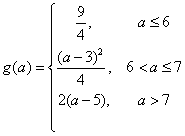

练习册系列答案
相关题目
 是连续的偶函数,且当
是连续的偶函数,且当 时,
时,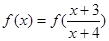 的所有
的所有 的和为 ( )
的和为 ( ) 是偶函数,且当
是偶函数,且当 时
时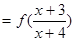 的所有
的所有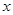 之和为 ▲
之和为 ▲  的函数
的函数 为偶函数,且当
为偶函数,且当 时,
时,
 ,
, ,则
,则 的大小关系是( )
的大小关系是( )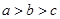 B.
B. C.
C. D.
D.
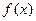 是偶
是偶 函数,且当
函数,且当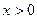 时
时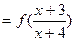 的所有
的所有 之和为 ▲
之和为 ▲