题目内容

（22）已知抛物线的焦点为F，A、B是抛物线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M。

    （I）证明为定值；

    （II）设的面积为S，写出的表达式，并求S的最小值。

解：

（Ⅰ）由已知条件，得

设由，

即得   

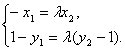
将①式两边平方并把代入得

      ③

解②、③式得，且有

抛物线方程为    求导得

所以过抛物线上A、B两点的切线方程分别是

，

即  

解出两条切线的交点M的坐标为

 

所以     

                  

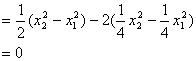
所以为定值，其值为0.


练习册系列答案
相关题目
已知抛物线的顶点在坐标原点，对称轴是坐标轴，并且经过点M(2，-2
2
)，求该抛物线的标准方程．
（2012•天津）已知抛物线的参数方程为
x=2pt2
y=2pt
（t为参数），其中p＞0，焦点为F，准线为l．过抛物线上一点M作l的垂线，垂足为E．若|EF|=|MF|，点M的横坐标是3，则p=
2
2
．
（22）已知抛物线．过动点M（，0）且斜率为1的直线与该抛物线交于不同的两点A、B，．

 

（Ⅰ）求的取值范围；

（Ⅱ）若线段AB的垂直平分线交轴于点N，求面积的最大值．
（22）已知抛物线．过动点M（，0）且斜率为1的直线与该抛物线交于不同的两点A、B．

（Ⅰ）若的取值范围；

（Ⅱ）若线段AB的垂直平分线交AB于点Q，交轴于点N，试求的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网