题目内容
将偶数按如图所示的规律排列下去,且用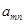 表示位于从上到下第
表示位于从上到下第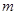 行,从左到右
行,从左到右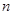 列的数,比如
列的数,比如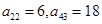 ,若
,若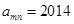 ,则有( )
,则有( )
A.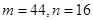 | B.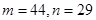 |
C.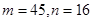 | D.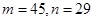 |
D
解析试题分析:从图中可以观察到,第一行有一个偶数,第二行有2个偶数,第三行有3个偶数, ,第 行有
行有 个偶数,所以前
个偶数,所以前 行共有
行共有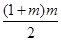 个偶数;又因为2014是从2开始的第1007个偶数,又因为
个偶数;又因为2014是从2开始的第1007个偶数,又因为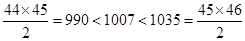 (这里并没有使用求解不等式
(这里并没有使用求解不等式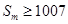 成立的最小正整数
成立的最小正整数 进行确定
进行确定 ,而是采用了简单二分法估算,如
,而是采用了简单二分法估算,如 ,
,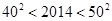 ,进而
,进而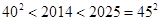 ,从而确定
,从而确定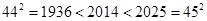 ,所以得到上面的不等式,或者根据选项中的数据直接确定上面的不等式也是一个明智的选择),所以可以确定
,所以得到上面的不等式,或者根据选项中的数据直接确定上面的不等式也是一个明智的选择),所以可以确定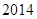 在第
在第 行,到
行,到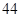 行时,总共才990个偶数,需要在第45行再找17个偶数,在第45行中是从中往左摆放偶数的,故2014处在从中往左算第17个偶数,从左往右算是第
行时,总共才990个偶数,需要在第45行再找17个偶数,在第45行中是从中往左摆放偶数的,故2014处在从中往左算第17个偶数,从左往右算是第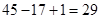 个数,所以
个数,所以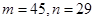 ,故选D.
,故选D.
考点:1.等差数列的前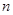 项和;2.估算法.
项和;2.估算法.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知数列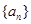 为等差数列,且
为等差数列,且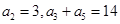 ,则
,则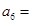 ( )
( )
| A.11 | B.12 | C.17 | D.20 |
等差数列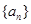 的公差是2,若
的公差是2,若 成等比数列,则
成等比数列,则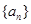 的前
的前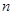 项和
项和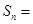 ( )
( )
A.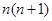 | B.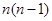 | C.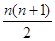 | D.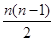 |
在等差数列 中,若
中,若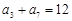 ,
, 是
是 的前
的前 项和,则
项和,则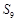 的值为
的值为
A.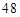 | B.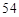 | C.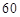 | D. |
已知数列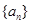 是等差数列,且
是等差数列,且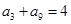 ,那么数列
,那么数列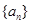 的前11项和等于( )
的前11项和等于( )
| A.22 | B.24 | C.44 | D.48 |
在等差数列3, 7, 11 …中,第5项为( )
| A.15 | B.18 | C.23 | D.19 |
已知等差数列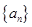 中,
中,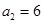 ,前
,前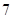 项和
项和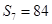 ,则
,则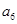 等于( )
等于( )
A.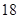 | B.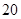 | C. | D.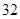 |
设等差数列{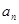 }的前n项和为Sn,若a1=1,a2+a3=11,则S6一S3=
}的前n项和为Sn,若a1=1,a2+a3=11,则S6一S3=
| A.27 | B.39 |
| C.45 | D.63 |
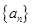 的前9项和
的前9项和 ,则
,则 .
.