题目内容
在数列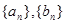 中,
中, ,且
,且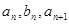 成等差数列,
成等差数列,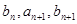 成等比数列
成等比数列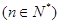 。
。
(1)求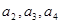 及
及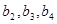 ,由此猜测
,由此猜测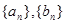 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明: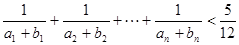 。
。
【答案】
(1)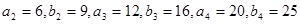 ,猜想
,猜想 ,(2)略
,(2)略
【解析】本试题主要是考查了数列的通项公式的求解,和数列的递推关系式的运用,以及数列求和的综合运用。
(1)利用已知的条件,对n赋值,然后得到数列的前几项,然后归纳猜想其通项公式。并运用数学归纳法加以证明。
(2)在第一问的基础上可知数列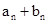 的表达式,然后利用裂项求和来证明不等式
的表达式,然后利用裂项求和来证明不等式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角
中,角 所对的边
所对的边 ,若
,若 ,则
,则