��Ŀ����
10����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��һ�����������������˵�����߹��ɵȱ������Σ�ֱ��x+$\sqrt{2}$y-2$\sqrt{3}$=0������ԲC���ҽ���FΪԲ�ģ�����Բ�Ķ̰��᳤Ϊ�뾶��Բ������1������ԲC�ķ��̣�
��2��������D��0��2������б��Ϊk��ֱ��l����ԲC�൱��M��N����
�����߶�MN���е�ĺ�����Ϊ1����ֱ��l�ķ��̣�
������F����MNΪֱ����Բ�ڲ�����ʵ��k��ȡֵ��Χ��
���� ��1��������֪��Բ�ķ���Ϊ��x-c��2+y2=b2��c=$\sqrt{3}$b��Բ�ĵ�ֱ��x+$\sqrt{2}$y-2$\sqrt{3}$=0�ľ���$\frac{|c-2\sqrt{3}|}{\sqrt{3}}$=b���������������������ԲC�ķ��̣�
��2������ֱ��l�ķ���Ϊy=kx+2��������Բ���̣�����Τ�ﶨ��������߶�MN���е�ĺ�����Ϊ1�����k��������ֱ��l�ķ��̣�
������F����MNΪֱ����Բ�ڲ���$\overrightarrow{FM}•\overrightarrow{FN}��0$��������ʵ��k��ȡֵ��Χ��
��� �⣺��1��������֪��Բ�ķ���Ϊ��x-c��2+y2=b2��c=$\sqrt{3}$b��
��Բ�ĵ�ֱ��x+$\sqrt{2}$y-2$\sqrt{3}$=0�ľ���$\frac{|c-2\sqrt{3}|}{\sqrt{3}}$=b��
��b=1��c=$\sqrt{3}$��
��a=2��
����ԲC�ķ���$\frac{{x}^{2}}{4}+{y}^{2}$=1��
��2����ֱ��l�ķ���Ϊy=kx+2��M��x1��y1����N��x2��y2��
ֱ�ߴ�����Բ���̣���ȥy�ɵã�1+4k2��x2+16kx+12=0
�ߡ�=��16k��2-4��12����1+4k2����0����k��-$\frac{\sqrt{3}}{2}$��k��$\frac{\sqrt{3}}{2}$
x1+x2=-$\frac{16k}{1+4{k}^{2}}$��x1x2=$\frac{12}{1+4{k}^{2}}$
�١��߶�MN���е�ĺ�����Ϊ1��
��x1+x2=-$\frac{16k}{1+4{k}^{2}}$=2��
��k=$\frac{-2��\sqrt{3}}{2}$��
��k��-$\frac{\sqrt{3}}{2}$��k��$\frac{\sqrt{3}}{2}$
��k=$\frac{-2+\sqrt{3}}{2}$��
��ֱ��l�ķ���y=$\frac{-2+\sqrt{3}}{2}$x+2��
������F����MNΪֱ����Բ�ڲ�����$\overrightarrow{FM}•\overrightarrow{FN}��0$��
�ࣨx1-$\sqrt{3}$��y1��•��x2-$\sqrt{3}$��y2��=��x1-$\sqrt{3}$����x2-$\sqrt{3}$��+y1y2��0
��y1y2=��kx1+2����kx2+2��=k2x1x2+2k��x1+x2��+4��
�ࣨ1+k2��x1x2+��2k-$\sqrt{3}$����x1+x2��+7��0
�ࣨ1+k2��$\frac{12}{1+4{k}^{2}}$+��2k-$\sqrt{3}$����-$\frac{16k}{1+4{k}^{2}}$��+7��0
��$\frac{-4\sqrt{3}-\sqrt{10}}{4}$��k��$\frac{-4\sqrt{3}+\sqrt{10}}{4}$��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�������ã�����ѧ���ļ��������������е��⣮

��һ������
| �ȼ� | ���� | �ϸ� | �д��Ľ� |
| Ƶ�� | 15 | x | 5 |
| �ȼ� | ���� | �ϸ� | �д��Ľ� |
| Ƶ�� | 15 | 3 | y |
��2���ɱ�һ������ͳ����������±�2��2�����������ж��Ƿ���90%�İ�����Ϊ����������������Ա��йء���
| ���� | Ů�� | �ܼ� | |
| ���� | 15 | 15 | 30 |
| ������ | |||
| �ܼ� | 45 |
| ��Ϊ��ҵ�� | ��Ϊ��ҵ���� | �ϼ� | |
| ϲ���������Ϸ | 18 | 9 | 27 |
| ��ϲ���������Ϸ | 8 | 15 | 23 |
| �ϼ� | 26 | 24 | 50 |
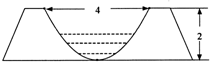 Ϊ��Ӧ��ũ�彨�裬ij��ƻ������о�ˮ�����и��죬��֪��ˮ���ĺ������һ��������������Ϊˮ����ˣ���ͼ��������Ϊ4m������Ϊ2m��
Ϊ��Ӧ��ũ�彨�裬ij��ƻ������о�ˮ�����и��죬��֪��ˮ���ĺ������һ��������������Ϊˮ����ˣ���ͼ��������Ϊ4m������Ϊ2m��