题目内容
 已知椭圆C:
已知椭圆C: =1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,
=1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,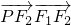 =0且△PF1F2的周长为6.
=0且△PF1F2的周长为6.
(Ⅰ)求椭圆C的方程和△PF1F2的外接圆D的方程;
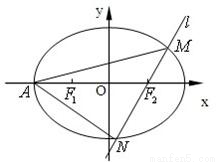
(Ⅱ)A为椭圆C的左顶点,过点F2的直线l与椭圆C交于M、N两点,且M、N均不在x轴上,设直线AM、AN的斜率分别为k1、k2,求k1•k2的值.
解:(Ⅰ)由已知得,c=1,2a+2=6,所以a=2,c=1
又a2=b2+c2,所以 ,椭圆C的方程为
,椭圆C的方程为
因为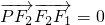 ,所以
,所以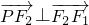 ,可求得P
,可求得P 或P
或P ,
,
所以Rt△PF2F1的外接圆D的方程是 或
或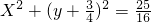 .
.
(Ⅱ)当直线l的斜率不存在时,由(Ⅰ)得M ,N
,N ,
,
可得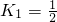 ,
,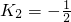 ,所以
,所以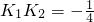 .
.
当直线l的斜率存在时,设其斜率为k,显然k≠0,
则直线l的方程为y=k(x-1),
设点M(x1,y1),N(x2,y2)将y=k(x-1)代入方程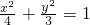 ,
,
并化简得:(3+4k2)x2-8k2x+4k2-12=0
可得:x1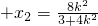 ,
,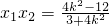 ,
,
所以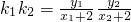 =
=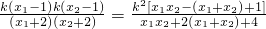 =
=
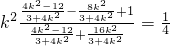 综上,
综上,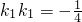 .
.
分析:(Ⅰ)根据焦点的坐标可求得c,进而根据三角形的周长求得a,则b可求得,进而求得椭圆C的方程,利用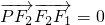 推断出两直线垂直,求得P的坐标,则Rt△PF2F1的外接圆D的方程可求得.
推断出两直线垂直,求得P的坐标,则Rt△PF2F1的外接圆D的方程可求得.
(Ⅱ)先看当直线的斜率不存在时,求得M,N则两直线的斜率可得,求得K1K2的值;再看斜率存在时,设出直线的方程与椭圆方程联立消去y,利用韦达定理表示出x1+x2和x1x2,代入到K1K2中,最后综合答案可得.
点评:本题主要考查圆、直线与椭圆的位置关系等基本知识,考查运算求解能力和分析问题、解决问题的能力.
又a2=b2+c2,所以
 ,椭圆C的方程为
,椭圆C的方程为
因为
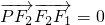 ,所以
,所以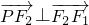 ,可求得P
,可求得P 或P
或P ,
,所以Rt△PF2F1的外接圆D的方程是
 或
或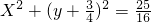 .
.(Ⅱ)当直线l的斜率不存在时,由(Ⅰ)得M
 ,N
,N ,
,可得
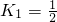 ,
,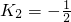 ,所以
,所以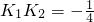 .
.当直线l的斜率存在时,设其斜率为k,显然k≠0,
则直线l的方程为y=k(x-1),
设点M(x1,y1),N(x2,y2)将y=k(x-1)代入方程
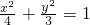 ,
,并化简得:(3+4k2)x2-8k2x+4k2-12=0
可得:x1
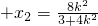 ,
,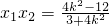 ,
,所以
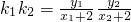 =
=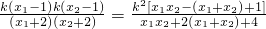 =
=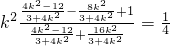 综上,
综上,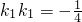 .
.分析:(Ⅰ)根据焦点的坐标可求得c,进而根据三角形的周长求得a,则b可求得,进而求得椭圆C的方程,利用
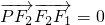 推断出两直线垂直,求得P的坐标,则Rt△PF2F1的外接圆D的方程可求得.
推断出两直线垂直,求得P的坐标,则Rt△PF2F1的外接圆D的方程可求得.(Ⅱ)先看当直线的斜率不存在时,求得M,N则两直线的斜率可得,求得K1K2的值;再看斜率存在时,设出直线的方程与椭圆方程联立消去y,利用韦达定理表示出x1+x2和x1x2,代入到K1K2中,最后综合答案可得.
点评:本题主要考查圆、直线与椭圆的位置关系等基本知识,考查运算求解能力和分析问题、解决问题的能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
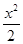 +y2=1的两焦点为
+y2=1的两焦点为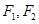 ,点
,点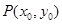 满足
满足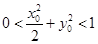 ,则|
,则|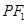 |+ç
|+ç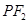 |的取值范围为____ ___.
|的取值范围为____ ___.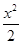 +y2=1的两焦点为
+y2=1的两焦点为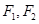 ,点
,点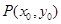 满足
满足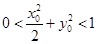 ,则|
,则|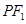 |+ç
|+ç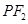 |的取值范围为____
___ .
|的取值范围为____
___ .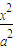 +
+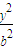 =1的两个焦点分别是F1(-1,0)、F2(1,0),且焦距是椭圆C上一点p到两焦点F1,F2距离的等差中项.
=1的两个焦点分别是F1(-1,0)、F2(1,0),且焦距是椭圆C上一点p到两焦点F1,F2距离的等差中项.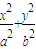 =1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,
=1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,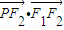 =0且△PF1F2的周长为6.
=0且△PF1F2的周长为6.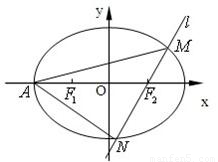
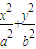 =1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,
=1的两个焦点的坐标分别为F1(-1,0)、F2(1,0),点P在椭圆上,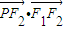 =0且△PF1F2的周长为6.
=0且△PF1F2的周长为6.