题目内容
已知矩形的两边长分别为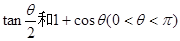
,且对任何
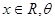都能使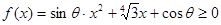
,则这些矩形的面积有最大值 ,最小值 。
有最大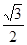值
,最小值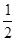
解析试题分析：根据题意，由于矩形的两边长分别为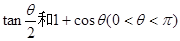,那么且对任何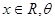都能使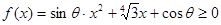,则可知判别式小于零，即可知
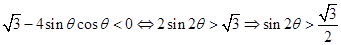，那么可知矩形的面积为S=
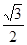，那么借助于三角函数的性质可知，面积有最大值,最小值。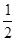
考点：三角函数性质
点评：主要考查了三角函数在几何图形中的运用，属于中档题。
练习册系列答案
相关题目
的部分图像如图所示，则将
的图象向右平移
个单位后，得到的图像解析式为________．
的定义域是 . 
，有下列命题：
为奇函数.
的最小正周期为2
.
对称,其中正确的命题序号为_____________.
的最小值为___________
有下列命题：
是以
为最小正周期的周期函数；
；
对称；
对称；其中正确的序号为 。
题目内容
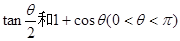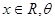已知矩形的两边长分别为,且对任何都能使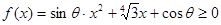,则这些矩形的面积有最大值 ,最小值 。
有最大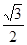值,最小值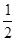
解析试题分析：根据题意，由于矩形的两边长分别为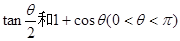,那么且对任何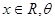都能使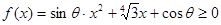,则可知判别式小于零，即可知 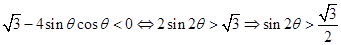，那么可知矩形的面积为S=，那么借助于三角函数的性质可知，面积有最大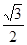值,最小值。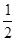
考点：三角函数性质
点评：主要考查了三角函数在几何图形中的运用，属于中档题。
，则
；
，
，
，
，且
，则
＝ .