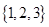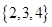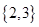题目内容
设集合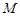 是
是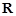 的子集,如果点
的子集,如果点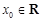 满足:
满足: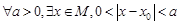 ,称
,称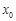 为集合
为集合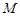 的聚点.则下列集合中以
的聚点.则下列集合中以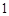 为聚点的有:①
为聚点的有:①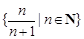 ; ②
; ②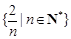 ; ③
; ③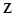 ; ④
; ④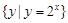 ( )
( )
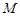 是
是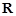 的子集,如果点
的子集,如果点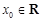 满足:
满足: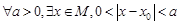 ,称
,称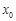 为集合
为集合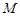 的聚点.则下列集合中以
的聚点.则下列集合中以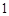 为聚点的有:①
为聚点的有:①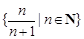 ; ②
; ②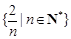 ; ③
; ③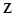 ; ④
; ④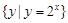 ( )
( )| A.①④ | B.②③ | C.①② | D.①②④ |
A
试题分析:①中,集合
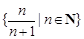 中的元素是极限为1的数列,∴在
中的元素是极限为1的数列,∴在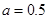 的时候,存在满足0<|x-1|<a的x,∴1是集合
的时候,存在满足0<|x-1|<a的x,∴1是集合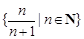 的聚点;②集合
的聚点;②集合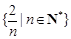 中的元素是极限为0的数列,最大值为2,即|x-1|≥1,对于某个a>1,不存在0<|x-1|
中的元素是极限为0的数列,最大值为2,即|x-1|≥1,对于某个a>1,不存在0<|x-1|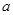 ,∴1不是集合
,∴1不是集合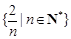 的聚点;③对于某个a<1,比如a=0.5,此时对任意的x∈Z,都有|x﹣1|=0或者|x﹣1|≥1,也就是说不可能0<|x﹣1|<0.5,从而1不是整数集Z的聚点;④
的聚点;③对于某个a<1,比如a=0.5,此时对任意的x∈Z,都有|x﹣1|=0或者|x﹣1|≥1,也就是说不可能0<|x﹣1|<0.5,从而1不是整数集Z的聚点;④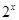 >0,存在0<|x-1|<0.5的数x,从而1是整数集Z的聚点,故选A.
>0,存在0<|x-1|<0.5的数x,从而1是整数集Z的聚点,故选A.
练习册系列答案
相关题目
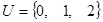 ,
, ,如果
,如果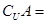
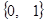 ,则
,则 .
. 相等的是( )
相等的是( )



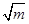 },B={1,m},A∪B=A,则m= ( ).
},B={1,m},A∪B=A,则m= ( ).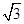
 ,
,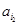 ,…,
,…,  },定义X的“特征数列”为x1,x2…,x100,其中
},定义X的“特征数列”为x1,x2…,x100,其中 =
=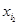 =…=
=…= =1.其余项均为0,例如子集{a2,a3}的“特征数列”为0,1,0,0,…,0 子集{a1,a3,a5}的“特征数列”的前三项和等于________________;若E的子集P的“特征数列”P1,P2,…,P100满足P1+Pi+1="1," 1≤i≤99;E 的子集Q的“特征数列”q1,q2,…,q100 满足q1=1,q1+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为___________.
=1.其余项均为0,例如子集{a2,a3}的“特征数列”为0,1,0,0,…,0 子集{a1,a3,a5}的“特征数列”的前三项和等于________________;若E的子集P的“特征数列”P1,P2,…,P100满足P1+Pi+1="1," 1≤i≤99;E 的子集Q的“特征数列”q1,q2,…,q100 满足q1=1,q1+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为___________.
 A∩B,A∩C=
A∩B,A∩C=

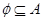

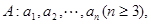 令
令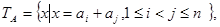
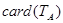 表示 集合
表示 集合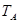 中元素个数.
中元素个数.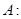 1,3,5,7,9,则
1,3,5,7,9,则 ,则
,则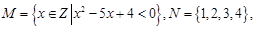 则
则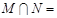 ( ).
( ).