题目内容
已知函数φ(x)=5x2+5x+1(x∈R),函数y=f(x)的图象与φ(x)的图象关于点(0, )中心对称.
)中心对称.
(1)求函数y=f(x)的解析式;
(2)如果g1(x)=f(x),gn(x)=f[gn-1(x)](n∈N,n≥2),试求出使g2(x)<0成立的x取值范围;
(3)是否存在区间E,使E∩{x|f(x)<0}=∅对于区间内的任意实数x,只要n∈N且n≥2时,都有gn(x)<0恒成立?
(本小题满分13分)
解:(1)∵函数y=f(x)的图象与φ(x)的图象关于点(0, )中心对称
)中心对称
∴f(x)=1-φ(-x)=1-(5x2-5x+1)=5x-5x2
(2)由g2(x)=5g1(x)-5g12(x)<0解得g1(x)<0或g1(x)>1
即5x-5x2<0或5x-5x2>1
解得x<0或x>1或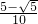 <x<
<x<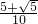
(3)由{x|f(x)<0}={x|x<0或x>1},
又(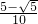 ,
,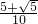 )∩{x|x<0或x>1}=∅,,
)∩{x|x<0或x>1}=∅,,
当x∈(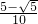 ,
,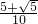 )时,g2(x)<0,g3(x)=5g2(x)-5g22(x)<0,
)时,g2(x)<0,g3(x)=5g2(x)-5g22(x)<0,
∴对于n=2,3时,E⊆(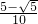 ,
,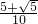 ),命题成立.
),命题成立.
以下用数学归纳法证明E⊆(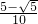 ,
,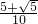 ),对n∈N,且n≥2时,都有gn(x)<0成立
),对n∈N,且n≥2时,都有gn(x)<0成立
假设n=k(k≥2,k∈N)时命题成立,即gk(x)<0,
那么gk+1(x)=f[gk(x)]=5gk(x)-5gk2(x)<0即n=k+1时,命题也成立.
∴存在满足条件的区间E⊆(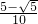 ,
,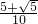 ).
).
分析:(1)根据函数y=f(x)的图象与φ(x)的图象关于点(0, )中心对称可得f(x)=1-φ(-x),可求出所求;
)中心对称可得f(x)=1-φ(-x),可求出所求;
(2)由g2(x)=5g1(x)-5g12(x)<0求出g1(x)的范围,然后可求出x的取值范围;
(3)根据(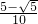 ,
,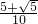 )∩{x|f(x)<0}=∅,验证n=2,3是否成立,然后利用数学归纳法进行证明即可.
)∩{x|f(x)<0}=∅,验证n=2,3是否成立,然后利用数学归纳法进行证明即可.
点评:本题主要考查了函数的对称性,以及不等式的解法和数学归纳法的应用,同时考查了运算求解的能力,属于中档题.
解:(1)∵函数y=f(x)的图象与φ(x)的图象关于点(0,
 )中心对称
)中心对称∴f(x)=1-φ(-x)=1-(5x2-5x+1)=5x-5x2
(2)由g2(x)=5g1(x)-5g12(x)<0解得g1(x)<0或g1(x)>1
即5x-5x2<0或5x-5x2>1
解得x<0或x>1或
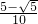 <x<
<x<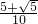
(3)由{x|f(x)<0}={x|x<0或x>1},
又(
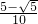 ,
,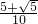 )∩{x|x<0或x>1}=∅,,
)∩{x|x<0或x>1}=∅,,当x∈(
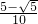 ,
,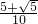 )时,g2(x)<0,g3(x)=5g2(x)-5g22(x)<0,
)时,g2(x)<0,g3(x)=5g2(x)-5g22(x)<0,∴对于n=2,3时,E⊆(
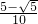 ,
,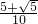 ),命题成立.
),命题成立.以下用数学归纳法证明E⊆(
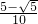 ,
,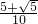 ),对n∈N,且n≥2时,都有gn(x)<0成立
),对n∈N,且n≥2时,都有gn(x)<0成立假设n=k(k≥2,k∈N)时命题成立,即gk(x)<0,
那么gk+1(x)=f[gk(x)]=5gk(x)-5gk2(x)<0即n=k+1时,命题也成立.
∴存在满足条件的区间E⊆(
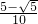 ,
,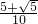 ).
).分析:(1)根据函数y=f(x)的图象与φ(x)的图象关于点(0,
 )中心对称可得f(x)=1-φ(-x),可求出所求;
)中心对称可得f(x)=1-φ(-x),可求出所求;(2)由g2(x)=5g1(x)-5g12(x)<0求出g1(x)的范围,然后可求出x的取值范围;
(3)根据(
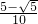 ,
,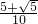 )∩{x|f(x)<0}=∅,验证n=2,3是否成立,然后利用数学归纳法进行证明即可.
)∩{x|f(x)<0}=∅,验证n=2,3是否成立,然后利用数学归纳法进行证明即可.点评:本题主要考查了函数的对称性,以及不等式的解法和数学归纳法的应用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
