题目内容
已知函数f(x)的部分图象如图所示,则函数f(x)的解析式为( )
A.f(x)=2sin( x+ x+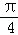 ) ) | B.f(x)=4sin( x+ x+ ) ) |
C.f(x)=2cos( x+ x+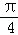 ) ) | D.f(x)=4sin( x+ x+ ) ) |
C
解析试题分析:结合函数f(x)的图象由利用特值法f(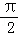 )=0,可排除某些项即可得到答案.
)=0,可排除某些项即可得到答案.
解:由函数f(x)的图象可知,f(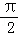 )=0,从而可排除A,D;
)=0,从而可排除A,D;
又f(﹣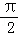 )=2,可排除B,
)=2,可排除B,
故选C.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,突出考查特值法与排除法的综合应用,考查分析与计算的能力,属于中档题.

练习册系列答案
相关题目
将函数y=2cos2x的图象向右平移 个单位长度,再将所得图象的所有点的横坐标缩短到原来的
个单位长度,再将所得图象的所有点的横坐标缩短到原来的 倍(纵坐标不变),得到的函数解析式为( )
倍(纵坐标不变),得到的函数解析式为( )
| A.y=cos2x | B.y=-2cosx | C.y=-2sin4x | D.y=-2cos4x |
已知点
 是圆
是圆 :
: 内任意一点,点
内任意一点,点 是圆上任意一点,则实数
是圆上任意一点,则实数 ( )
( )
| A.一定是负数 | B.一定等于0 | C.一定是正数 | D.可能为正数也可能为负数 |
若函数 满足f(1)=0,则( )
满足f(1)=0,则( )
| A.f(x-2)—定是奇函数 | B.f(x+1)—定是偶函数 |
| C.f(x+3)一定是偶函数 | D.f(x-3)一定是奇函数 |
已知函数 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则 的值不可能是 ( )
的值不可能是 ( )
A. | B. | C.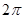 | D. |
已知函数 ,若存在
,若存在 ,使得
,使得 恒成立,则
恒成立,则 的值是( )
的值是( )
A.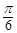 | B. | C. | D. |
已知 ,则角
,则角 = ( )
= ( )
A. | B. | C. | D. |
已知函数
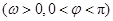 的图象如图所示 ,则
的图象如图所示 ,则 等于( )
等于( )
A. | B. | C. | D. |
 的图象向左平移
的图象向左平移 个单位,再向上平移2个单位,则所得函数的表达式是( )
个单位,再向上平移2个单位,则所得函数的表达式是( )


