题目内容
对于复数z1=m（m-1）+（m-1）i，z2=（m+1）+（m2-1）i，（m∈R）（1）若z1是纯虚数，求m的值；
（2）若z2在复平面内对应的点位于第四象限，求m的取值范围；
（3）若z1，z2都是虚数，且
| OZ1 |
| OZ2 |
分析：（1）复数为纯虚数的条件是：实部等于0，且虚部不等于0．
（2） z2在复平面内对应的点位于第四象限，说明 z2的实部大于0，且虚部小于0．
（3）z1，z2都是虚数，说明z1，z2的虚部都不等于0，再利用两个向量的数量积公式求出 m的值，代入复数模的计算公式求值．
（2） z2在复平面内对应的点位于第四象限，说明 z2的实部大于0，且虚部小于0．
（3）z1，z2都是虚数，说明z1，z2的虚部都不等于0，再利用两个向量的数量积公式求出 m的值，代入复数模的计算公式求值．
解答：解：（1）∵复数z1=m（m-1）+（m-1）i，z1是纯虚数，∴m（m-1）=0，且（m-1）≠0，∴m=0．
（2）∵z2在复平面内对应的点位于第四象限，z2=（m+1）+（m2-1）i，（m∈R）
∴（m+1）＞0，且（m2-1）＜0，∴-1＜m＜1．
（3）∵z1，z2都是虚数，∴（m-1）≠0，且 （m2-1）≠0，即 m≠±1，
∵
•
=0，∴m（m-1）•（m+1）+（m-1）•（m2-1）=0，
（m-1）（2m2+m-1）=0，∴（2m2+m-1）=0，m=
，
|z1+z2|=|（m2+1）+（m2 +m-2）i|=|
-
i|=
．
（2）∵z2在复平面内对应的点位于第四象限，z2=（m+1）+（m2-1）i，（m∈R）
∴（m+1）＞0，且（m2-1）＜0，∴-1＜m＜1．
（3）∵z1，z2都是虚数，∴（m-1）≠0，且 （m2-1）≠0，即 m≠±1，
∵
| OZ1 |
| OZ2 |
（m-1）（2m2+m-1）=0，∴（2m2+m-1）=0，m=
| 1 |
| 2 |
|z1+z2|=|（m2+1）+（m2 +m-2）i|=|
| 5 |
| 4 |
| 5 |
| 4 |
5
| ||
| 4 |
点评：本题考查复数代数形式的混合运算，以及复数的基本概念的应用．
练习册系列答案
相关题目
=____________;z·
=____________.?
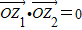，求|z1+z2|．