题目内容
设函数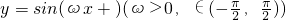 的最小正周期为π,且其图象关于直线
的最小正周期为π,且其图象关于直线 对称,则在下面四个结论中:(1)图象关于点
对称,则在下面四个结论中:(1)图象关于点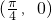 对称;(2)图象关于点
对称;(2)图象关于点 对称;(3)在
对称;(3)在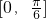 上是增函数;(4)在
上是增函数;(4)在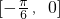 上是增函数,那么所有正确结论的编号为________.
上是增函数,那么所有正确结论的编号为________.
解:因为函数最小正周期为 =π,故ω=2
=π,故ω=2
再根据图象关于直线 对称,得出
对称,得出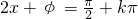
取 ,得φ=
,得φ=
所以函数表达式为: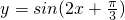
当 时,函数值
时,函数值 ,因此函数图象关于点
,因此函数图象关于点 对称
对称
所以(2)是正确的
解不等式:
得函数的增区间为:
所以(4)正确的.
故答案为(2)(4)
分析:首先由三角函数周期公式和对称轴方程,求出ω=2和φ= ,然后再由三角函数图象关于对称性的规律:对称轴处取最值,对称中心为零点.由此再结合函数的最小正周期,则不难从(1)、(2)中选出.再解一个不等式:
,然后再由三角函数图象关于对称性的规律:对称轴处取最值,对称中心为零点.由此再结合函数的最小正周期,则不难从(1)、(2)中选出.再解一个不等式: ,取适当的k值,就可以从(3)、(4)中选出是(4)正确的.
,取适当的k值,就可以从(3)、(4)中选出是(4)正确的.
点评:本题着重考查了三角函数的周期性、对称性和单调性,属于中档题.熟悉三角函数的图象与性质,能对正余弦曲线进行合理地变形,找出其中的规律所在,是解决本题的关键.
 =π,故ω=2
=π,故ω=2再根据图象关于直线
 对称,得出
对称,得出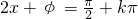
取
 ,得φ=
,得φ=
所以函数表达式为:
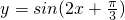
当
 时,函数值
时,函数值 ,因此函数图象关于点
,因此函数图象关于点 对称
对称所以(2)是正确的
解不等式:

得函数的增区间为:

所以(4)正确的.
故答案为(2)(4)
分析:首先由三角函数周期公式和对称轴方程,求出ω=2和φ=
 ,然后再由三角函数图象关于对称性的规律:对称轴处取最值,对称中心为零点.由此再结合函数的最小正周期,则不难从(1)、(2)中选出.再解一个不等式:
,然后再由三角函数图象关于对称性的规律:对称轴处取最值,对称中心为零点.由此再结合函数的最小正周期,则不难从(1)、(2)中选出.再解一个不等式: ,取适当的k值,就可以从(3)、(4)中选出是(4)正确的.
,取适当的k值,就可以从(3)、(4)中选出是(4)正确的.点评:本题着重考查了三角函数的周期性、对称性和单调性,属于中档题.熟悉三角函数的图象与性质,能对正余弦曲线进行合理地变形,找出其中的规律所在,是解决本题的关键.

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 ,则( )
,则( ) 在
在 单调递减
B.
单调递减
B. 单调递增
单调递增  的最小正周期为
的最小正周期为 .
. 的最小正值.
的最小正值. 的图像是由
的图像是由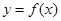 的图像向右平移
的图像向右平移 个单位长度得到,求
个单位长度得到,求 的最小正周期为
的最小正周期为 ,则
,则 在
在 单调递减
B.
单调递减
B. 单调递增
单调递增  的最小正周期为
的最小正周期为 .
.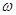 的值.
的值. 的图像是由
的图像是由 的图像向右平移
的图像向右平移 个单位长度得到,求
个单位长度得到,求