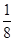题目内容
已知公差不为零的等差数列的第k、n、p项构成等比数列的连续三项,则等比数列的公比为( )
分析:设首项和公差,由等比数列的性质可知q=
=
=
,然后利用等差数列的通项公式化简即可.
| an |
| ak |
| ap |
| an |
| ap-an |
| an-ak |
解答:解:设等差数列首项为a1,公差为d,则
q=
=
=
=
=
=
.
故选A.
q=
| an |
| ak |
| ap |
| an |
| ap-an |
| an-ak |
=
| [a1+(p-1)d]-[a1+(n-1)d] |
| [a1+(n-1)d]-[a1+(k-1)d] |
| p-n |
| n-k |
| n-p |
| k-n |
故选A.
点评:此题考查了等比数列和等差数列的性质,属于基础题.

练习册系列答案
相关题目
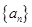 与公比为
与公比为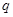 的等比数列
的等比数列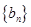 有相同的首项,同时满足
有相同的首项,同时满足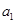 ,
,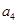 ,
,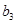 成等比,
成等比, ,
,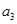 ,
,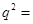 ( )
( )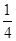 B.
B.
 C.
C.
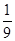 D.
D.