题目内容
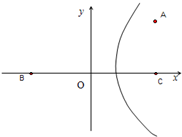A村在C村正北| 3 |
（1）如图，以BC中点O为原点，建立坐标系，求弧形公路PQ所在曲线的方程；
（2）现要在公路旁建造一个变电站M分别向A村、C村送电，但A村有一村办工厂用电需用专用线路，不得与民用混线用电，因此向A村要架两条线路分别给村民和工厂送电．要使用电线最短，变电站M应建在A村的什么方位，并求出M到A村的距离．
分析：（1）以线段BC所在直线为x轴，其垂直平分线为y轴，建立直角坐标系．根据题意得PQ上任一点到B、C两点的距离之差为8km，结合双曲线的定义得出动点在以B，C为焦点，实轴长为8的双曲线上，从而求得弧形公路PQ所在曲线的方程；
（2）依题意，即求2|MA|+|MC|的最小值．过A作AN垂直于右准线于N，设t=2|MA|+|MC|=2（|MA|+d）≥2|AN|，由平面几何知识知，当M为AN与双曲线交点时，t最小，从而解决问题．
（2）依题意，即求2|MA|+|MC|的最小值．过A作AN垂直于右准线于N，设t=2|MA|+|MC|=2（|MA|+d）≥2|AN|，由平面几何知识知，当M为AN与双曲线交点时，t最小，从而解决问题．
解答：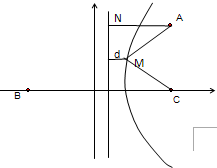
解：（1）（6分）以线段BC所在直线为x轴，其垂直平分线为y轴，建立直角坐标系．
∵PQ上任一点到B、C两点的距离之差为8km
由双曲线定义，PQ所在曲线为双曲线的右支，
B、C为焦点，c=8，a=4
∴b2=c2-a2=64-16=48，…（4分）
∴所求方程为：
-
=1（x＞0）…（6分）（没有范围扣1分）
（2）（7分）依题意，即求2|MA|+|MC|的最小值…（1分）
由第二定义
=e=
=
=2（d为M到右准线的距离）
∴|MC|=2d，过A作AN垂直于右准线于N，
设t=2|MA|+|MC|=2（|MA|+d）≥2|AN|．则当M为AN与双曲线交点时，t最小…（3分）
∵A（8，
）∴yM=
，代入双曲线方程，得xM=
，…（5分）
此时M在A的正西方向，|MA|=8-
∴应把电房建在A村正西方向距离A村8-
km处使得电线最短…（7分）
解：（1）（6分）以线段BC所在直线为x轴，其垂直平分线为y轴，建立直角坐标系．∵PQ上任一点到B、C两点的距离之差为8km
由双曲线定义，PQ所在曲线为双曲线的右支，
B、C为焦点，c=8，a=4
∴b2=c2-a2=64-16=48，…（4分）
∴所求方程为：
| x2 |
| 16 |
| y2 |
| 48 |
（2）（7分）依题意，即求2|MA|+|MC|的最小值…（1分）
由第二定义
| |MC| |
| d |
| c |
| a |
| 8 |
| 4 |
∴|MC|=2d，过A作AN垂直于右准线于N，
设t=2|MA|+|MC|=2（|MA|+d）≥2|AN|．则当M为AN与双曲线交点时，t最小…（3分）
∵A（8，
| 3 |
| 3 |
| 17 |
此时M在A的正西方向，|MA|=8-
| 17 |
∴应把电房建在A村正西方向距离A村8-
| 17 |
点评：考查圆锥曲线的实际背景及作用、考查学生根据实际问题选择函数类型的能力，以及会用双曲线的定义的方法来求函数的最小值的能力．
练习册系列答案
阅读快车系列答案
相关题目
如图，A村在B地正北