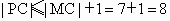题目内容
(2007
辽宁,20)已知正三角形OAB的三个顶点都在抛物线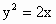 上,其中O为坐标原点,设圆C是△OAB的外接圆(点C为圆心).
上,其中O为坐标原点,设圆C是△OAB的外接圆(点C为圆心).
(1)
求圆C的方程;(2)
设圆M的方程为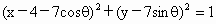 ,
,
过圆
M上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求 的最大值和最小值.
的最大值和最小值.
答案:略
解析:
提示:
解析:
|
解析: (1)设A、B两点坐标分别为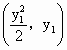 , , ,由题设知 ,由题设知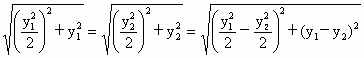 , ,
解得 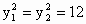 .所以A .所以A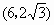 ,B ,B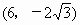 或A 或A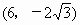 ,B ,B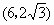 . .
设圆心 C的坐标为(r,0),则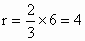 . .
因此圆 C的方程为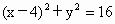 . .
(2) 设∠ECF=2α,则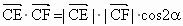 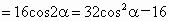 . .
在 Rt△PCE中,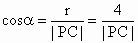 .由圆的几何性质得 .由圆的几何性质得
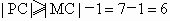 . .
所以 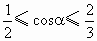 ,由此可得 ,由此可得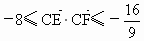 . .
故 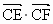 的最大值为 的最大值为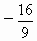 ,最小值为-8. ,最小值为-8. |
提示:
|
剖析:本题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力. |

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目