Question

在△ABC中，角、、的对边分别为、、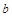，设S为△ABC的面积，满足．

(Ⅰ)求角C的大小；

(Ⅱ)若，且，求的值．

 

Answer 1

【答案】

(I)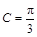;(II)4.

【解析】

试题分析：(Ⅰ)本小题较易，直接利用余弦定理及三角形面积公式，确定，

根据，得到；

（Ⅱ）应用“切化弦”技巧，转化成“弦函数”问题，应用正弦定理可得，进一步求得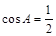，得到，确定得到△ABC是等边三角形，根据 可求得.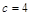

试题解析： (Ⅰ) 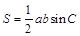，且.  2分

因为，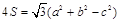

所以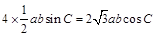，  3分

所以，  4分

因为，

所以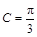；  6分

（Ⅱ）由得：

，   7分

即，  8分

又由正弦定理得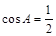，  9分

∴，

∴△ABC是等边三角形，  10分

∴，  11分

所以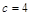.  12分

考点：正弦定理、余弦定理的应用，三角形面积公式，平面向量的数量积.