题目内容
(本小题满分14分)
已知位于 轴右侧的圆C与
轴右侧的圆C与 相切于点P(0,1),与
相切于点P(0,1),与 轴相交于点A、B,且被
轴相交于点A、B,且被 轴分成的两段弧之比为1﹕2(如图所示).
轴分成的两段弧之比为1﹕2(如图所示).
(I)求圆C的方程;
(II)若经过点(1,0)的直线 与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线
与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线 的方程.
的方程.
已知位于
 轴右侧的圆C与
轴右侧的圆C与 相切于点P(0,1),与
相切于点P(0,1),与 轴相交于点A、B,且被
轴相交于点A、B,且被 轴分成的两段弧之比为1﹕2(如图所示).
轴分成的两段弧之比为1﹕2(如图所示).(I)求圆C的方程;
(II)若经过点(1,0)的直线
 与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线
与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线 的方程.
的方程.
解:(I)因为圆C位于 轴右侧,且与
轴右侧,且与 相切于点P(0,1),
相切于点P(0,1),
所以圆心C在直线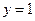 上.
上.
又圆C被 轴分成的两段弧之比为1﹕2,所以
轴分成的两段弧之比为1﹕2,所以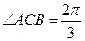 . ……………………….3分
. ……………………….3分
所以PC=AC=BC=2,圆心C的坐标为(2,1).
所求圆C的方程为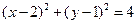 . ……………………………………………6分(II)①若直线
. ……………………………………………6分(II)①若直线 斜率存在,设直线
斜率存在,设直线 的方程为
的方程为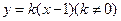 ,即
,即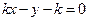 .
.
因为线段EF为直径的圆恰好过圆心C,所以EC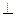 FC.
FC.
因此 . …………………………………………………………………8分
. …………………………………………………………………8分
圆心C(2,1)到直线 的距离
的距离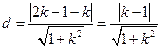 .
.
由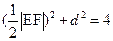 得
得 .
.
故所求直线 的方程为
的方程为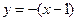 ,即
,即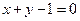 . ………………………11分
. ………………………11分
②若直线 斜率不存在,此时直线
斜率不存在,此时直线 的方程为
的方程为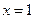 ,点E、F的坐标分别为
,点E、F的坐标分别为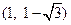 、
、 ,可以验证不满足条件. …………………………………………..13分
,可以验证不满足条件. …………………………………………..13分
故所求直线的方程为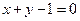 . ……………………………………14分
. ……………………………………14分
 轴右侧,且与
轴右侧,且与 相切于点P(0,1),
相切于点P(0,1),所以圆心C在直线
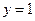 上.
上.又圆C被
 轴分成的两段弧之比为1﹕2,所以
轴分成的两段弧之比为1﹕2,所以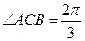 . ……………………….3分
. ……………………….3分所以PC=AC=BC=2,圆心C的坐标为(2,1).
所求圆C的方程为
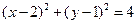 . ……………………………………………6分(II)①若直线
. ……………………………………………6分(II)①若直线 斜率存在,设直线
斜率存在,设直线 的方程为
的方程为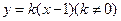 ,即
,即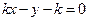 .
.因为线段EF为直径的圆恰好过圆心C,所以EC
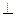 FC.
FC.因此
 . …………………………………………………………………8分
. …………………………………………………………………8分圆心C(2,1)到直线
 的距离
的距离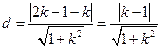 .
.由
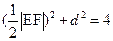 得
得 .
. 故所求直线
 的方程为
的方程为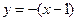 ,即
,即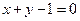 . ………………………11分
. ………………………11分②若直线
 斜率不存在,此时直线
斜率不存在,此时直线 的方程为
的方程为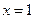 ,点E、F的坐标分别为
,点E、F的坐标分别为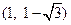 、
、 ,可以验证不满足条件. …………………………………………..13分
,可以验证不满足条件. …………………………………………..13分故所求直线的方程为
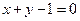 . ……………………………………14分
. ……………………………………14分略

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 中,
中, 是斜边上的高线,
是斜边上的高线, 则
则 为( ).
为( ).



 ABC中,若sinAsinB<cosAcosB,则
ABC中,若sinAsinB<cosAcosB,则 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 。
。 .
. ,求.
,求.  中,过中线
中,过中线 中点
中点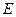 任作一直线分别交
任作一直线分别交 于
于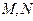 两点,设
两点,设 ,则
,则 的最小值是 .
的最小值是 .
 和
和 ,第一排和最后一排的距离
,第一排和最后一排的距离 米(如图所示),旗杆底部与第一排在一个水平面上.
米(如图所示),旗杆底部与第一排在一个水平面上. 秒,升旗手应以 (米 /秒)的速度匀速升旗.
秒,升旗手应以 (米 /秒)的速度匀速升旗.
 中
中 , 已知
, 已知  ,
,  ,
, ,则
,则 ( )
( )



 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知
 求
求 的值。
的值。 中,∠A:∠B=1:2,∠
中,∠A:∠B=1:2,∠ 的平分线
的平分线 分⊿ACD与⊿BCD的面积比是3:2,
分⊿ACD与⊿BCD的面积比是3:2,