题目内容
下面四个不等式:
(1)a2+b2+c2≥ab+bc+ac;
(2)a(1-a)≤ ;
;
(3) +
+ ≥2;
≥2;
(4)(a2+b2)(c2+d2)≥(ac+bd)2;
其中恒成立的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:作差,进而可以因式分解,从而得到完全平方式,故可证(1)(4),根据基本不等式可证(2),(3)可利用取特殊值进行判定.
解答:(1)a2+b2+c2-ab-ac-bc
= (2a2+2b2+2c2-2ab-2ac-2bc)
(2a2+2b2+2c2-2ab-2ac-2bc)
= [(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)]
[(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)]
= [(a-b)2+(b-c)2+(a-c)2]≥0,故恒成立;
[(a-b)2+(b-c)2+(a-c)2]≥0,故恒成立;
(2)a(1-a)≤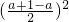 =
= ,故恒成立;
,故恒成立;
(3)当a=1,b=-1时,不等式不成立,故不恒成立;
(4)∵(a2+b2)(c2+d2)-(ac+bd)2=a2c2+a2d2+b2c2+b2d2-(a2c2+b2d2+2acbd)
=a2d2+b2c2-2acbd=(ad-bc)2≥0则(a2+b2)(c2+d2)≥(ac+bd)2,故恒成立;
故选C.
点评:本题主要考查了基本不等式的证明,以及配方法的应用,同时考查了计算能力,属于基础题.
分析:作差,进而可以因式分解,从而得到完全平方式,故可证(1)(4),根据基本不等式可证(2),(3)可利用取特殊值进行判定.
解答:(1)a2+b2+c2-ab-ac-bc
=
 (2a2+2b2+2c2-2ab-2ac-2bc)
(2a2+2b2+2c2-2ab-2ac-2bc)=
 [(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)]
[(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)]=
 [(a-b)2+(b-c)2+(a-c)2]≥0,故恒成立;
[(a-b)2+(b-c)2+(a-c)2]≥0,故恒成立;(2)a(1-a)≤
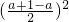 =
= ,故恒成立;
,故恒成立;(3)当a=1,b=-1时,不等式不成立,故不恒成立;
(4)∵(a2+b2)(c2+d2)-(ac+bd)2=a2c2+a2d2+b2c2+b2d2-(a2c2+b2d2+2acbd)
=a2d2+b2c2-2acbd=(ad-bc)2≥0则(a2+b2)(c2+d2)≥(ac+bd)2,故恒成立;
故选C.
点评:本题主要考查了基本不等式的证明,以及配方法的应用,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目

 ,有下面四个不等式:(1)
,有下面四个不等式:(1) ;(2)a<b (3)a+b<ab;
(4)
;(2)a<b (3)a+b<ab;
(4) ,不正确的不等式的个数是( )
,不正确的不等式的个数是( )