题目内容
(本大题满分14分)
已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于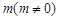 .
.
(Ⅰ)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点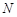 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合).求证直线
不重合).求证直线 与
与 轴的交点为定点,并求出该定点的坐标.
轴的交点为定点,并求出该定点的坐标.
【答案】
(1) (1) 当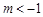 时 轨迹
时 轨迹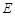 表示焦点在
表示焦点在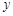 轴上的椭圆,且除去
轴上的椭圆,且除去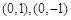 两点;
两点;
当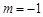 时 轨迹
时 轨迹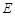 表示以
表示以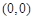 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去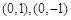 两点;
两点;
当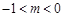 时 轨迹
时 轨迹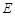 表示焦点在
表示焦点在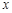 轴上的椭圆,且除去
轴上的椭圆,且除去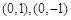 两点;
两点;
当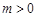 时 轨迹
时 轨迹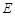 表示焦点在
表示焦点在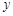 轴上的双曲线,且除去
轴上的双曲线,且除去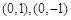 两点
两点
(2) 直线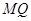 过定点
过定点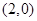
【解析】
试题分析:(Ⅰ)由题知: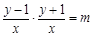
化简得: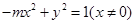 ……………………………2分
……………………………2分
当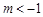 时 轨迹
时 轨迹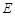 表示焦点在
表示焦点在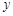 轴上的椭圆,且除去
轴上的椭圆,且除去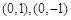 两点;
两点;
当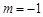 时 轨迹
时 轨迹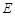 表示以
表示以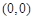 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去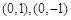 两点;
两点;
当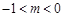 时 轨迹
时 轨迹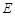 表示焦点在
表示焦点在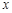 轴上的椭圆,且除去
轴上的椭圆,且除去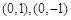 两点;
两点;
当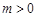 时 轨迹
时 轨迹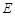 表示焦点在
表示焦点在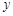 轴上的双曲线,且除去
轴上的双曲线,且除去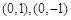 两点;
两点;
……………………………6分
(Ⅱ)设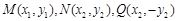
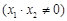
依题直线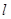 的斜率存在且不为零,则可设
的斜率存在且不为零,则可设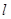 :
: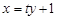 ,
,
代入 整理得
整理得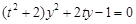
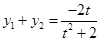 ,
,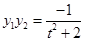 , ………………………………9分
, ………………………………9分
又因为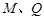 不重合,则
不重合,则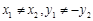

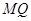 的方程为
的方程为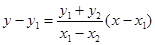 令
令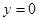 ,
,
得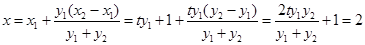
故直线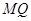 过定点
过定点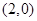 . ……………………………13分
. ……………………………13分
解二:设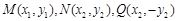
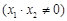
依题直线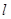 的斜率存在且不为零,可设
的斜率存在且不为零,可设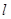 :
: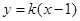
代入 整理得:
整理得:
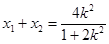 ,
,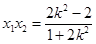 , ……………………………9分
, ……………………………9分

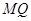 的方程为
的方程为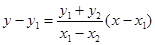 令
令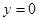 ,
,
得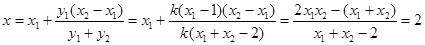
 直线
直线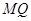 过定点
过定点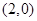 ……………………………13分
……………………………13分
考点:考查了圆锥曲线方程,以及直线与圆锥曲线的位置关系
点评:解决含参数的曲线方程的问题,主要是关注我们方程的特点来分类讨论得到,同时能结合设而不求的思想求解坐标,进而求解直线方程,属于中档题。

练习册系列答案
相关题目
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用 ,
, ,当
,当 为何值时,
为何值时,
 与
与
 和
和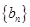 满足:
满足: ,
, ,
,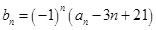 ,其中
,其中 为实数,
为实数, 为正整数.
为正整数. 时,数列
时,数列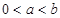 (
( 为实常数),
为实常数),  为数列
为数列 ?若存在,求
?若存在,求 过椭圆C:
过椭圆C: 的右焦点F,
的右焦点F, 上的射影依次为点D、E.
上的射影依次为点D、E. 
 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点;
为x轴上一点;