题目内容
(本小题满分13分)已知函数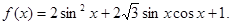 求:
求:
(1)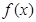 的最小正周期;(2)
的最小正周期;(2)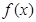 的单调递增区间;(3)
的单调递增区间;(3)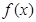 在
在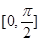 上的最值.
上的最值.
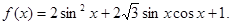 求:
求:(1)
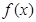 的最小正周期;(2)
的最小正周期;(2)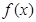 的单调递增区间;(3)
的单调递增区间;(3)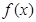 在
在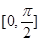 上的最值.
上的最值.(1)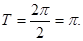 (2)
(2)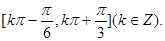 (3)
(3)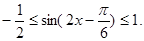
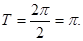 (2)
(2)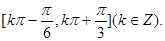 (3)
(3)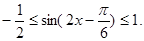
(1)先根据二倍角和两角和差的正余弦公式化简函数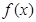 ,进而利用公式求出最小正周期;(2)代入正弦函数的单调递增区间即可求解函数f(x)的单调增区间;(3)根据已知求出角的范围,再利用函数的单调性求出函数的值域。
,进而利用公式求出最小正周期;(2)代入正弦函数的单调递增区间即可求解函数f(x)的单调增区间;(3)根据已知求出角的范围,再利用函数的单调性求出函数的值域。
解:(Ⅰ)因为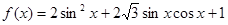
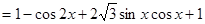
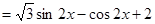
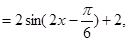
所以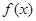 的最小正周期
的最小正周期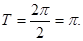
(Ⅱ)因为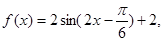
所以由
得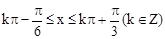
所以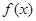 的单调增区间是
的单调增区间是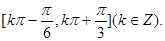
(Ⅲ)因为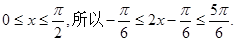
所以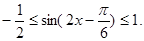
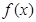 ,进而利用公式求出最小正周期;(2)代入正弦函数的单调递增区间即可求解函数f(x)的单调增区间;(3)根据已知求出角的范围,再利用函数的单调性求出函数的值域。
,进而利用公式求出最小正周期;(2)代入正弦函数的单调递增区间即可求解函数f(x)的单调增区间;(3)根据已知求出角的范围,再利用函数的单调性求出函数的值域。解:(Ⅰ)因为
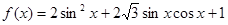
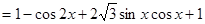
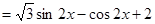
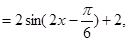
所以
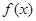 的最小正周期
的最小正周期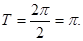
(Ⅱ)因为
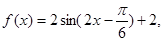
所以由

得
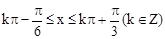
所以
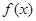 的单调增区间是
的单调增区间是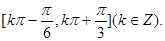
(Ⅲ)因为
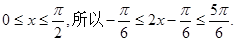
所以
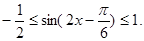

练习册系列答案
相关题目
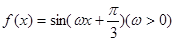 在
在 上恰有一个最高点和一个最低点,求
上恰有一个最高点和一个最低点,求 的取值范围
的取值范围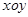 中,角
中,角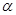 的顶点为坐标原点,始边在
的顶点为坐标原点,始边在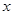 轴的正半轴上,当角
轴的正半轴上,当角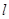 :
: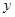 =3
=3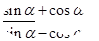 的值; (2)
的值; (2)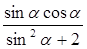 的值.
的值. ,
,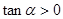 ,则
,则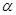 的终边在( )
的终边在( ) ,则cos2α=
,则cos2α=



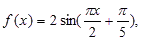 对任意的
对任意的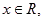 都有
都有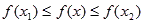 成立,则
成立,则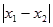 的最小值为( )
的最小值为( )


 π,θ]上的最大值为1,则θ的值是( )
π,θ]上的最大值为1,则θ的值是( )

 是锐角,
是锐角, ,则
,则 ;
;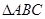 中,已知
中,已知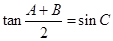 ,则
,则