题目内容
14.已知函数$f(x)=cos(\frac{π}{2}-x)cosx+\sqrt{3}{sin^2}x$(Ⅰ)求f(x)的最小正周期及单调递减区间;
(Ⅱ)求$x∈[\frac{π}{6},\frac{π}{2}]$时函数f(x)的最大值和最小值.
分析 (1)化简得f(x)=sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$.令$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,解出单调递减区间;
(2)根据x的范围求出2x-$\frac{π}{3}$的范围,结合正弦函数的单调性求出最值.
解答 解:(1)f(x)=sinxcosx+$\sqrt{3}$•$\frac{1-cos2x}{2}$=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{2}$
=sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$.
∴f(x)的最小正周期是T=π.
令$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,解得$\frac{5π}{12}$+kπ≤x≤$\frac{11π}{12}$+kπ,
∴f(x)的单调减区间是[$\frac{5π}{12}$+kπ,$\frac{11π}{12}$+kπ],k∈Z.
(2)∵$x∈[\frac{π}{6},\frac{π}{2}]$,∴2x-$\frac{π}{3}$∈[0,$\frac{2π}{3}$],
∴当2x-$\frac{π}{3}$=0 时,f(x)取得最小值$\frac{\sqrt{3}}{2}$,
当2x-$\frac{π}{3}$=$\frac{π}{2}$ 时,f(x)取得最大值$\frac{\sqrt{3}}{2}$+1.
点评 本题综合考查三角公式,三角恒等变形等知识,属于中档题.

练习册系列答案
相关题目
4.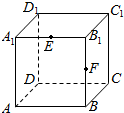 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )| A. | AD上 | B. | B1C1上 | C. | A1D1上 | D. | BC上 |
2.点A、B、C、D在同一个球的球面上,${A}{B}={B}C=\sqrt{2}$,AC=2,若四面体ABCD体积的最大值为$\frac{2}{3}$,则这个球的表面积为( )
| A. | 8π | B. | $\frac{25π}{4}$ | C. | $\frac{25π}{16}$ | D. | $\frac{125π}{6}$ |
6.f(x)是定义在R上的奇函数,且f(3)>f(1),下列各式一定成立的是( )
| A. | f(0)<f(4) | B. | f(-3)<f(-1) | C. | f(-1)<f(-3) | D. | f(3)>f(0) |
4.已知正三棱锥P-ABC中,底边AB=8,顶角∠APB=90°,则过P、A、B、C四点的球体的表面积是( )
| A. | 384π | B. | 192π | C. | 96π | D. | 24π |