题目内容
在四面体
中，AB，AC，AD两两垂直，AB=
,AD=2,AC=
，则该四面体外接球的表面积为 ．
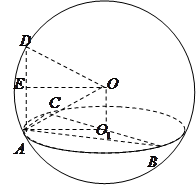
解析试题分析：方法一:设
为球心，因为
所以
所在截面圆的直径为
，取中点
，则 为截面圆圆心，所以
圆面，又
所以
圆面，所以
∥
又
所以
∥
四边形
是平行四边形 ，所以
，在直角三角形
中，
，所以
.
方法二：由球的对称性及
两两垂直可以补形为长方体
,长方体的对称中心即为球心, 所以
所以 . 
考点：球及线面关系的应用.
练习册系列答案
阅读快车系列答案
相关题目
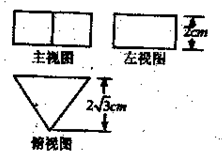
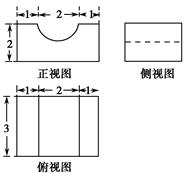
中，
,
，规定主视方向为垂直于平面
的方向，则可求得三棱柱左视图的面积为 ； 
，则该几何体的体积为 
