题目内容
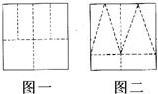
将一边长为4的正方形纸片按照图中的虚线所示的方法剪开后拼接为一正四棱锥,则该正四棱锥的体积为
分析:由已知中将一边长为4的正方形纸片按照图中的虚线所示的方法剪开后拼接为一正四棱锥,我们可以求出拼接后四棱锥的底面棱长为原正方形边长的一半,四棱锥的则高为原正方形边长的
,进而求出棱锥的底面面积和高,代入棱锥体积公式,即可求出答案.
| 3 |
| 4 |
解答:解:由已知中正方形纸片的边长为4,
故四棱锥的底面棱长为2,
则四棱的底面面积S=2×2=4
则四棱锥的侧高为3
则四棱锥的高H=
=2
则正四棱锥的体积V=
•S•H=
故答案为:
.
故四棱锥的底面棱长为2,
则四棱的底面面积S=2×2=4
则四棱锥的侧高为3
则四棱锥的高H=
| 32-12 |
| 2 |
则正四棱锥的体积V=
| 1 |
| 3 |
8
| ||
| 3 |
故答案为:
8
| ||
| 3 |
点评:本题考查的知识点是棱锥的体积,其中根据已知确定棱锥的棱长,侧高,底面积及高是解答本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
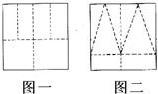 将一边长为4的正方形纸片按图一中的虚线所示的方法剪开后拼成一个正四棱柱,设其体积为V1;若将同样的正方形按图二中的虚线所示的方法剪开后拼成一个正四棱锥,设其体积为V2,则V1与V2的大小关系是
将一边长为4的正方形纸片按图一中的虚线所示的方法剪开后拼成一个正四棱柱,设其体积为V1;若将同样的正方形按图二中的虚线所示的方法剪开后拼成一个正四棱锥,设其体积为V2,则V1与V2的大小关系是