题目内容
下列函数的图象,经过平移或翻折后不能与函数y=log2x的图象重合的函数是( )
| A、y=2x | ||
B、y=log
| ||
C、y=
| ||
D、y=log2
|
分析:从自己熟悉的知识入手,易知A、y=log2x与y=2x互为反函数,则图象关于y=x对称;B、y=log
x=-log2x易知是y=log2x变换而来的;C、两个函数的底不同;D、y=log2
+1=-log2x+1易知是y=log2x变换而来的.
| 1 |
| 2 |
| 1 |
| x |
解答:解:A、易知:y=log2x与y=2x互为反函数,
则图象关于y=x对称,两者图象翻折得到.
B、∵y=log
x=-log2x
∴关于x轴对称,两者图象翻折得到
D、y=log2
+1=-log2x+1与y=log2x图象关于x轴对称,再向上平移一个单位.
两者图象翻折再平移得到.
C、两个函数的底不同不会由变换得到.
故选C
则图象关于y=x对称,两者图象翻折得到.
B、∵y=log
| 1 |
| 2 |
∴关于x轴对称,两者图象翻折得到
D、y=log2
| 1 |
| x |
两者图象翻折再平移得到.
C、两个函数的底不同不会由变换得到.
故选C
点评:本题主要考查数形结合的思想,函数解析式有内在联系,则图象间有变换关系,同样,图象间有变换关系,则函数间有内在联系,在探讨过程中作适当的等价变形是很重要的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 •4x
•4x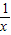 +1
+1