题目内容
如果函数y=a2x+2ax-1(a>0且a≠1)在[-1,1]上有最大值14,试求a的值.
设t=ax,则原函数可化为y=(t+1)2-2,对称轴为t=-1.
(1)若a>1,∵x∈[-1,1],
∴-1<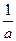 ≤t≤a.
≤t≤a.
∵t=ax在[-1,1]上递增,
∴y=(t+1)2-2当t∈[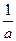 ,a]时也递增.
,a]时也递增.
∴原函数在[-1,1]上递增.
故当x=1时,ymax=a2+2a-1.
由a2+2a-1=14,解得a=3或a=-5(舍去,因a>1).
(2)若1>a>0,可得当x=-1时,ymax=a-2+2a-1-1=14,
解得a=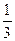 或a=-
或a=- (舍去).
(舍去).
综上,a=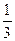 或3.
或3.
(1)若a>1,∵x∈[-1,1],
∴-1<
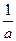 ≤t≤a.
≤t≤a.∵t=ax在[-1,1]上递增,
∴y=(t+1)2-2当t∈[
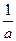 ,a]时也递增.
,a]时也递增.∴原函数在[-1,1]上递增.
故当x=1时,ymax=a2+2a-1.
由a2+2a-1=14,解得a=3或a=-5(舍去,因a>1).
(2)若1>a>0,可得当x=-1时,ymax=a-2+2a-1-1=14,
解得a=
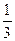 或a=-
或a=- (舍去).
(舍去).综上,a=
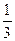 或3.
或3.将原函数看成是二次函数和指数函数合成的复合函数,利用相应函数的性质及复合函数的单调性解题.可采用换元法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
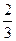 )=
)=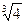 ,则f(-
,则f(-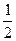 )=______________.
)=______________.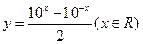
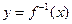

 )1-x
)1-x

 ,求证:
,求证: .
. 满足
满足 ,则
,则 的最小值为 ( )
的最小值为 ( ) .
. B.
B. C.
C. D.
D.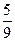
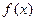 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当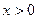 时,
时,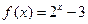 ,则
,则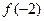 =( )
=( )


 (2)
(2)