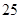题目内容
已知向量 ,则A、B、C三点构成三角形是
,则A、B、C三点构成三角形是
 的( )
的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:根据向量加法的三角形法则证明充分性成立,由特殊情况 共线时判断必要性不成立.
共线时判断必要性不成立.
解答:解:由向量加法的三角形法则得,当A、B、C三点构成三角形时,
有 成立,即充分性成立;
成立,即充分性成立;
当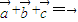 时,
时,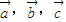 共线时,
共线时,
A,B,C三点不能构成三角形,则必要性不成立.
故选A.
点评:本题考查了向量加法的三角形法则以及充要条件的判断,可以利用特殊情况进行判断充分性和必要性是否成立.
 共线时判断必要性不成立.
共线时判断必要性不成立.解答:解:由向量加法的三角形法则得,当A、B、C三点构成三角形时,
有
 成立,即充分性成立;
成立,即充分性成立;当
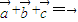 时,
时,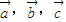 共线时,
共线时,A,B,C三点不能构成三角形,则必要性不成立.
故选A.
点评:本题考查了向量加法的三角形法则以及充要条件的判断,可以利用特殊情况进行判断充分性和必要性是否成立.

练习册系列答案
相关题目
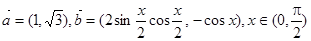 ,若
,若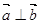 ,则
,则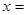
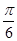 B.
B.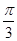 C.
C.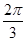 D.
D.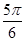
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.