题目内容
图中多面体是经过正四棱柱底面顶点B作截面A1BC1D1而截得的,已知AA1=CC1,截面A1BC1D1与底面ABCD成45°的二面角,AB=1,则这个多面体的体积为( )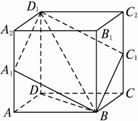
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:以正方形ABCD为底面,DD1为棱将上图补成一个正四棱柱ABCD—A2B1C2D1 ,如图所示.?

∵截面A1BC1D1与底面ABCD成45°的二面角,?
∴原多面体的体积恰好为补成的正四棱柱体积的一半.?
∵AA1=CC1,易知∠D1BD为截面与底面ABCD所成的二面角的平面角.?
∴∠D1BD=45°.?
∵AB=1,∴BD=![]() ,DD1=
,DD1=![]() .?
.?
∴正四棱柱ABCD—A2B1C2D1的体积V=1×![]() =
=![]() .?
.?
∴所求多面体的体积为![]() .
.
答案:A

练习册系列答案
相关题目