题目内容
以下四个命题:
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质;
②(1+x)n=a0+a1x+a2x2+…+anxn,且a1+a2+…+an=63则展开式中系数最大的项是20x3
③12名同学合影,站成了前排4人后排8人.现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 C82A62
④Sk=
+
+
+…+
(k=1,2,3,…),则Sk+1=Sk+
-
其中正确命题的序号是( )
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质;
②(1+x)n=a0+a1x+a2x2+…+anxn,且a1+a2+…+an=63则展开式中系数最大的项是20x3
③12名同学合影,站成了前排4人后排8人.现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 C82A62
④Sk=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
其中正确命题的序号是( )
分析:①根据类比推理进行判断.②利用二项展开式的基本定理确定n的数值.③利用排列和组合的知识求解.④利用数列的通项公式判断.
解答:解:①根据类比推理可知由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质,所以①正确.
②由二次展开式可知,a0=1,当x=1时,有2n=a0+a1+a2+…+an=1+63=64,解得n=6,
所以二项式系数最大为
x3=20x3,所以②正确.
③从后排8人中选2人共C82种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,所以为A62,则不同调整方法的种数是C82A62,所以③正确.
④因为Sk+1=
+
+…+
+
+
,
所以Sk+1=
+
+…+
+
+
-
=Sk+
+
-
=Sk+
-
,所以④正确.
故选D.
②由二次展开式可知,a0=1,当x=1时,有2n=a0+a1+a2+…+an=1+63=64,解得n=6,
所以二项式系数最大为
| C | 3 6 |
③从后排8人中选2人共C82种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,所以为A62,则不同调整方法的种数是C82A62,所以③正确.
④因为Sk+1=
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
所以Sk+1=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
=Sk+
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
故选D.
点评:本题主要考查命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则
,则 ;
; ;
;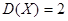 ,则
,则 .
.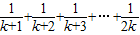 (k=1,2,3,…),则Sk+1=Sk+
(k=1,2,3,…),则Sk+1=Sk+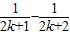
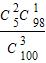 ;
;